题目内容
(2013•重庆)在平面上,
⊥
,|
|=|
|=1,
=
+
.若|
|<
,则|
|的取值范围是( )
| AB1 |
| AB2 |
| OB1 |
| OB2 |
| AP |
| AB1 |
| AB2 |
| OP |
| 1 |
| 2 |
| OA |
分析:建立坐标系,将向量条件用等式与不等式表示,利用向量模的计算公式,即可得到结论.
解答: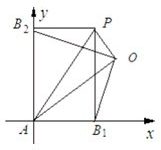 解:根据条件知A,B1,P,B2构成一个矩形A,B1PB2,以AB1,AB2所在直线为坐标轴建立直角坐标系,设|AB1|=a,|AB2|=b,点O的坐标为(x,y),则点P的坐标为(a,b),
解:根据条件知A,B1,P,B2构成一个矩形A,B1PB2,以AB1,AB2所在直线为坐标轴建立直角坐标系,设|AB1|=a,|AB2|=b,点O的坐标为(x,y),则点P的坐标为(a,b),
由|
|=|
|=1,得
,则
∵|
|<
,∴(x-a)2+(y-b)2<
∴1-x2+1-y2<
∴x2+y2>
①
∵(x-a)2+y2=1,∴y2=1-(x-a)2≤1,
∴y2≤1
同理x2≤1
∴x2+y2≤2②
由①②知
<x2+y2≤2,
∵|
|=
,∴
<|
|≤
故选D.
 解:根据条件知A,B1,P,B2构成一个矩形A,B1PB2,以AB1,AB2所在直线为坐标轴建立直角坐标系,设|AB1|=a,|AB2|=b,点O的坐标为(x,y),则点P的坐标为(a,b),
解:根据条件知A,B1,P,B2构成一个矩形A,B1PB2,以AB1,AB2所在直线为坐标轴建立直角坐标系,设|AB1|=a,|AB2|=b,点O的坐标为(x,y),则点P的坐标为(a,b),由|
| OB1 |
| OB2 |
|
|
∵|
| OP |
| 1 |
| 2 |
| 1 |
| 4 |
∴1-x2+1-y2<
| 1 |
| 4 |
∴x2+y2>
| 7 |
| 4 |
∵(x-a)2+y2=1,∴y2=1-(x-a)2≤1,
∴y2≤1
同理x2≤1
∴x2+y2≤2②
由①②知
| 7 |
| 4 |
∵|
| OA |
| x2+y2 |
| ||
| 2 |
| OA |
| 2 |
故选D.
点评:本题考查向量知识的运用,考查学生转化问题的能力,考查学生的计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
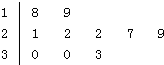 (2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )
(2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )