题目内容
(2013•重庆)在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.若极坐标方程为ρcosθ=4的直线与曲线
(t为参数)相交于A,B两点,则|AB|=
|
16
16
.分析:先将直线极坐标方程ρcosθ=4化成直角坐标方程,再代入曲线
(t为参数)中得A,B两点的直角坐标,最后利用两点间的距离公式即可得出|AB|.
|
解答:解:将直线极坐标方程ρcosθ=4化成直角坐标方程为x=4,代入曲线
(t为参数)中得A,B两点的直角坐标为(4,8),(4,-8),
则|AB|=16.
故答案为:16.
|
则|AB|=16.
故答案为:16.
点评:本题考查参数方程、极坐标方程、直角坐标方程间的转化,两点间的距离公式,考查转化、计算能力.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
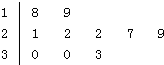 (2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )
(2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )