题目内容
(2013•重庆)在△ABC中,内角A,B,C的对边分别是a,b,c,且a2+b2+
ab=c2.
(1)求C;
(2)设cosAcosB=
,
=
,求tanα的值.
| 2 |
(1)求C;
(2)设cosAcosB=
3
| ||
| 5 |
| cos(α+A)cos(α+B) |
| cos2α |
| ||
| 5 |
分析:(1)利用余弦定理表示出cosC,将已知等式变形后代入求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数;
(2)已知第二个等式分子两项利用两角和与差的余弦函数公式化简,再利用同角三角函数间的基本关系弦化切,利用多项式乘多项式法则计算,由A+B的度数求出sin(A+B)的值,进而求出cos(A+B)的值,利用两角和与差的余弦函数公式化简cos(A+B),将cosAcosB的值代入求出sinAsinB的值,将各自的值代入得到tanα的方程,求出方程的解即可得到tanα的值.
(2)已知第二个等式分子两项利用两角和与差的余弦函数公式化简,再利用同角三角函数间的基本关系弦化切,利用多项式乘多项式法则计算,由A+B的度数求出sin(A+B)的值,进而求出cos(A+B)的值,利用两角和与差的余弦函数公式化简cos(A+B),将cosAcosB的值代入求出sinAsinB的值,将各自的值代入得到tanα的方程,求出方程的解即可得到tanα的值.
解答:解:(1)∵a2+b2+
ab=c2,即a2+b2-c2=-
ab,
∴由余弦定理得:cosC=
=
=-
,
又C为三角形的内角,
则C=
;
(2)由题意
=
=
,
∴(cosA-tanαsinA)(cosB-tanαsinB)=
,
即tan2αsinAsinB-tanα(sinAcosB+cosAsinB)+cosAcosB=tan2αsinAsinB-tanαsin(A+B)+cosAcosB=
,
∵C=
,A+B=
,cosAcosB=
,
∴sin(A+B)=
,cos(A+B)=cosAcosB-sinAsinB=
-sinAsinB=
,即sinAsinB=
,
∴
tan2α-
tanα+
=
,即tan2α-5tanα+4=0,
解得:tanα=1或tanα=4.
| 2 |
| 2 |
∴由余弦定理得:cosC=
| a2+b2-c2 |
| 2ab |
-
| ||
| 2ab |
| ||
| 2 |
又C为三角形的内角,
则C=
| 3π |
| 4 |
(2)由题意
| cos(α+A)cos(α+B) |
| cos2α |
| (cosαcosA-sinαsinA)(cosαcosB-sinαsinB) |
| cos2α |
| ||
| 5 |
∴(cosA-tanαsinA)(cosB-tanαsinB)=
| ||
| 5 |
即tan2αsinAsinB-tanα(sinAcosB+cosAsinB)+cosAcosB=tan2αsinAsinB-tanαsin(A+B)+cosAcosB=
| ||
| 5 |
∵C=
| 3π |
| 4 |
| π |
| 4 |
3
| ||
| 5 |
∴sin(A+B)=
| ||
| 2 |
3
| ||
| 5 |
| ||
| 2 |
| ||
| 10 |
∴
| ||
| 10 |
| ||
| 2 |
3
| ||
| 5 |
| ||
| 5 |
解得:tanα=1或tanα=4.
点评:此题考查了余弦定理,两角和与差的余弦函数公式,同角三角函数间的基本关系,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
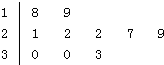 (2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )
(2013•重庆)如图是某公司10个销售店某月销售某产品数量(单位:台)的茎叶图,则数据落在区间[22,30)内的概率为( )