题目内容
设函数f(x)=| 1 |
| 2 |
| 2x+t |
| x2-3 |
(1)求函数g(x)在区间(-∞,-a)上单调区间,并说明理由;
(2)若曲线g(x)在x=1处的切线斜率为-4,且方程g(x)-m=0有两上不等的负实根,求m的取值范围.
分析:(1)据极值点处的导数为0,利用二次方程的根与系数的关系将g′(x)用a,b表示,令g′(x)>0得到单增区间;令令g′(x)<0得到单减区间
(2)据在切点处的导数值为切线斜率,求出t的值,通过求g(x)的单调性及极值画出g(x)的大致图象,数形结合求出m的取值范围.
(2)据在切点处的导数值为切线斜率,求出t的值,通过求g(x)的单调性及极值画出g(x)的大致图象,数形结合求出m的取值范围.
解答: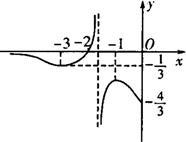 解:(1)令f′(x)=x-t+
解:(1)令f′(x)=x-t+
=
=0
∴a,b为方程x2-tx+3=0的两根,
又g′(x)=-
=
=(x≠±
)
由0<a<b及ab=3知0<a<
<b,
∴-b<-
<-a<0,
当x∈(-b,-a)且x≠-
时,g′(x)>0;当x∈(-∞,-b)时,g′(x)<0
∴g(x)在(-∞,-b)上单调递减;在区间(-b,-
),(-
,-a)上单调递增
(2)由g′(1)=-
=-4得t=4
∴g(x)=
,
∴g′(x)=
,
令g′(x0=0解得x=-3或-1
∴当x在(-∞,0]上变化时,g(x),g′(x)的变化情况如下:
当x<-3时,g′(x)<0;
当-3<x<-
时,g′(x)>0;
当-
< x<-1时,g′(x)>0;
当-1<x<0时,g′(x)<0
故当x=-3时,有极小值-
;
当x=-1时,有极大值-1;并且g(0)=-
∴g(x)的大致图象为:
∴方程g(x)-m=0有两个不等的负实根时,m∈(-
,-1)∪(-
,0)
 解:(1)令f′(x)=x-t+
解:(1)令f′(x)=x-t+| 3 |
| x |
| x2-tx+3 |
| x |
∴a,b为方程x2-tx+3=0的两根,
又g′(x)=-
| 2(x2+tx+3) |
| (x2-3)2 |
| -2(x+a)(x+b) |
| (x2-3)2 |
| 3 |
由0<a<b及ab=3知0<a<
| 3 |
∴-b<-
| 3 |
当x∈(-b,-a)且x≠-
| 3 |
∴g(x)在(-∞,-b)上单调递减;在区间(-b,-
| 3 |
| 3 |
(2)由g′(1)=-
| 2(t+4) |
| 4 |
∴g(x)=
| 2x+4 |
| x2-3 |
∴g′(x)=
| -2(x+1)(x+3) |
| (x2-3)2 |
令g′(x0=0解得x=-3或-1
∴当x在(-∞,0]上变化时,g(x),g′(x)的变化情况如下:
当x<-3时,g′(x)<0;
当-3<x<-
| 3 |
当-
| 3 |
当-1<x<0时,g′(x)<0
故当x=-3时,有极小值-
| 1 |
| 3 |
当x=-1时,有极大值-1;并且g(0)=-
| 4 |
| 3 |
∴g(x)的大致图象为:
∴方程g(x)-m=0有两个不等的负实根时,m∈(-
| 4 |
| 3 |
| 1 |
| 3 |
点评:本题考查通过导数求函数极值,求单调区间;画函数的大致图象等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设函数f(x)=
,若f(a)<1,则实数a的取值范围是( )
|
| A、(-∞,-3) |
| B、(1,+∞) |
| C、(-3,1) |
| D、(-∞,-3)∪(1,+∞) |
设函数f(x)=
,若f(x0)>2,则x0的取值范围是( )
|
| A、(-1,4) |
| B、(-1,+∞) |
| C、(4,+∞) |
| D、(-∞,-1)∪(4,+∞) |
 设函数
设函数