题目内容
半径为 的球面上有
的球面上有 、
、 、
、 三点,已知
三点,已知 和
和 间的球面距离为
间的球面距离为 ,
, 和
和 ,
, 和
和 的球面距离都为
的球面距离都为 ,求
,求 、
、 、
、 三点所在的圆面与球心的距离.
三点所在的圆面与球心的距离.
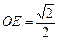
解析解:设球心为O,连结OA,OB,OC,AB,AC,BC,则由A、B、C、O形成一个三棱锥.
因为A和C间的球面距离为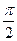 ,所以
,所以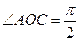 ;
;
同理由A和B,B和C的球面距离都为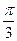 ,有
,有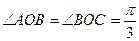 ,
,
且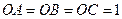 ,…w.w.^w.k.&s.5*u.c.#om………………………………(6分)
,…w.w.^w.k.&s.5*u.c.#om………………………………(6分)
如图,则有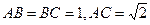 ,所以
,所以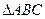 是等腰直角三角形;
是等腰直角三角形;
因为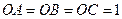 ,则点O在平面ABC的射影是
,则点O在平面ABC的射影是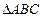 的外心.……(9分)
的外心.……(9分)
而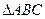 是等腰直角三角形,其外心是斜边AC的中点,设中点为E,连结OE,则线段OE的长度是点O到平面ABC的距离.
是等腰直角三角形,其外心是斜边AC的中点,设中点为E,连结OE,则线段OE的长度是点O到平面ABC的距离.
对 ,
,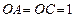 ,
,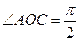 ,易知
,易知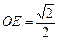 .
.

练习册系列答案
相关题目
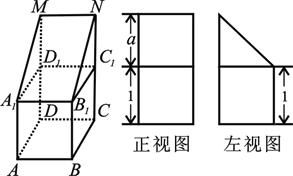
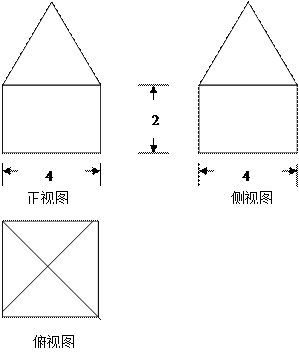
(本小题满分13分)如图,在正方体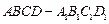 的上底面上叠放三棱柱
的上底面上叠放三棱柱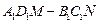 ,该几何体的正视图与左视图如右图所示.
,该几何体的正视图与左视图如右图所示.
(Ⅰ)若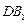
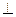
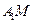 ,求实数
,求实数 的值;K^S*5U.C#O
的值;K^S*5U.C#O
(Ⅱ)在(I)的条件下:
① 证明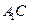
 平面
平面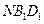 ;
;
②求直线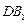 与平面
与平面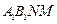 所成角的正弦值
所成角的正弦值
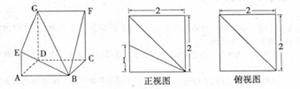
如图所示,正三棱锥 中,
中, 分别是
分别是 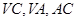 的中点,
的中点,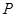 为
为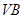 上任意一点,则直线
上任意一点,则直线 与
与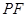 所成的角的大小是 ( )
所成的角的大小是 ( )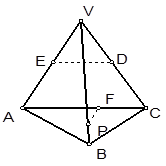
A.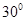 | B.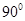 | C.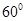 | D.随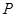 点的变化而变化. 点的变化而变化. |
如图,在斜三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在( )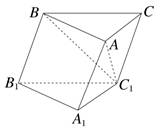
| A.直线AB上 | B.直线BC上 |
| C.直线AC上 | D.△ABC内部 |
 ,深为
,深为 ,宽为
,宽为 ,池壁的造价为
,池壁的造价为 ,求水池的总造价。
,求水池的总造价。
 中,平面
中,平面 平面
平面 ,
, ,
, 是等边三角形,已知
是等边三角形,已知 ,
, .
. (Ⅰ)设
(Ⅰ)设 是
是 上的一点,证明:平面
上的一点,证明:平面 平面
平面 ;
;
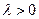 使得
使得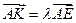 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为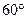 ,求
,求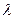 的值。
的值。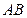 所在直线方程为
所在直线方程为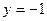 ,线段
,线段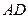 所在直线方程为
所在直线方程为 ,线段
,线段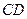 所在直线方程为
所在直线方程为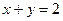 ,求四边形
,求四边形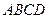 绕
绕 所在直线旋转一周所围成的几何体的表面积和体积
所在直线旋转一周所围成的几何体的表面积和体积