题目内容
已知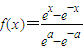 ,若函数f(x)在R上是减函数,则实数a的取值范围是 .
,若函数f(x)在R上是减函数,则实数a的取值范围是 .
【答案】分析:由题意可得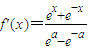 ,因为函数f(x)在R上是减函数,所以
,因为函数f(x)在R上是减函数,所以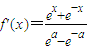 <0在R上恒成立.因为ex+e-x>0,所以ea-e-a<0,进而得到答案.
<0在R上恒成立.因为ex+e-x>0,所以ea-e-a<0,进而得到答案.
解答:解:由题意可得:函数为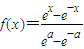 ,
,
所以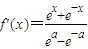 .
.
因为函数f(x)在R上是减函数,
所以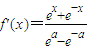 <0在R上恒成立.
<0在R上恒成立.
因为ex+e-x>0,
所以ea-e-a<0,
解得a<0.
故答案为a<0.
点评:解决此类问题的关键是熟练掌握求导公式,以及利用导数判断函数的单调性与球函数的单调区间问题.
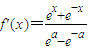 ,因为函数f(x)在R上是减函数,所以
,因为函数f(x)在R上是减函数,所以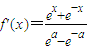 <0在R上恒成立.因为ex+e-x>0,所以ea-e-a<0,进而得到答案.
<0在R上恒成立.因为ex+e-x>0,所以ea-e-a<0,进而得到答案.解答:解:由题意可得:函数为
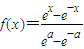 ,
,所以
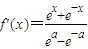 .
.因为函数f(x)在R上是减函数,
所以
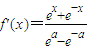 <0在R上恒成立.
<0在R上恒成立.因为ex+e-x>0,
所以ea-e-a<0,
解得a<0.
故答案为a<0.
点评:解决此类问题的关键是熟练掌握求导公式,以及利用导数判断函数的单调性与球函数的单调区间问题.

练习册系列答案
相关题目
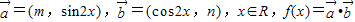 ,若函数f(x)的图象经过点(0,1)和
,若函数f(x)的图象经过点(0,1)和 .
.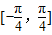 上的最大值与最小值之和为3,求a的值.
上的最大值与最小值之和为3,求a的值.
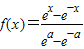 ,若函数f(x)在R上是减函数,则实数a的取值范围是 .
,若函数f(x)在R上是减函数,则实数a的取值范围是 .