题目内容
(2012•眉山一模)设函数f(x)对其定义域内的任意实数x1与x2都有f(
)≥
,则称函数f(x)为上凸函数. 若函数f(x)为上凸函数,则对定义域内任意x1、x2、x3,…,xn都有f(
)≥
(当x1=x2=x3=…=xn时等号成立),称此不等式为琴生不等式,现有下列命题:
①f(x)=lnx(x>0)是上凸函数;
②二次函数f(x)=ax2+bx+c(a≠0)是上凸函数的充要条件是a>0;
③f(x)是上凸函数,若A(x1,f(x1)),B(x2,f(x2))是f(x)图象上任意两点,点C在线段AB上,且
=λ
,则f(
)≥
;
④设A,B,C是一个三角形的三个内角,则sinA+sinB+sinC的最大值是
.
其中,正确命题的序号是
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| x1+x2+…+xn |
| n |
| f(x1)+f(x2)+…+f(xn) |
| n |
①f(x)=lnx(x>0)是上凸函数;
②二次函数f(x)=ax2+bx+c(a≠0)是上凸函数的充要条件是a>0;
③f(x)是上凸函数,若A(x1,f(x1)),B(x2,f(x2))是f(x)图象上任意两点,点C在线段AB上,且
| AC |
| CB |
| x1+λx2 |
| 1+λ |
| f(x1)+λf(x2) |
| 1+λ |
④设A,B,C是一个三角形的三个内角,则sinA+sinB+sinC的最大值是
3
| ||
| 2 |
其中,正确命题的序号是
①③④
①③④
(写出所有你认为正确命题的序号).分析:作图可知①正确,②不正确.对于③,如图,因为f(x)上凸函数,则点C在点D的下方,点C的纵坐标为
,点D的坐标为(
,f(
)),故f(
)≥f(
).对于④,因为f(x)=sinx在(0,
)上是凸函数,由琴生不等式知
≥
.
| f(x1)+λf(x2) |
| 1+λ |
| x1+λx2 |
| 1+λ |
| x1+λx2 |
| 1+λ |
| x1+λx2 |
| 1+λ |
| x1+λx2 |
| 1+λ |
| π |
| 2 |
| ||
| 2 |
| sinA+sinB+sinC |
| 3 |
解答: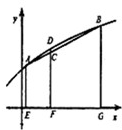 解:作图可知①正确,②不正确.
解:作图可知①正确,②不正确.
对于③,如图,因为f(x)上凸函数,则点C在点D的下方,点C的纵坐标为
,
点D的坐标为(
,f(
)),
于是得f(
)≥f(
),即③正确.
对于④,因为f(x)=sinx在(0,
)上是凸函数,
由琴生不等式知sin
≥
,
即
≥
,
所以sinA+sinB+sinC≤
,
当A=B=C时,取④正确.
综上所述,正确命题是①③④.
 解:作图可知①正确,②不正确.
解:作图可知①正确,②不正确.对于③,如图,因为f(x)上凸函数,则点C在点D的下方,点C的纵坐标为
| f(x1)+λf(x2) |
| 1+λ |
点D的坐标为(
| x1+λx2 |
| 1+λ |
| x1+λx2 |
| 1+λ |
于是得f(
| x1+λx2 |
| 1+λ |
| x1+λx2 |
| 1+λ |
对于④,因为f(x)=sinx在(0,
| π |
| 2 |
由琴生不等式知sin
| A+B+C |
| 3 |
| sinA+sinB+sinC |
| 3 |
即
| ||
| 2 |
| sinA+sinB+sinC |
| 3 |
所以sinA+sinB+sinC≤
3
| ||
| 2 |
当A=B=C时,取④正确.
综上所述,正确命题是①③④.
点评:本题考查命题真假的判断与应用,解题时要认真审题,注意数形结合思想的灵活运用,挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目