题目内容
如图,四棱锥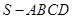 的底面是正方形,侧棱
的底面是正方形,侧棱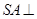 底面
底面 ,过
,过 作
作 垂直
垂直 交
交 于
于 点,作
点,作 垂直
垂直 交
交 于
于 点,平面
点,平面 交
交 于
于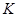 点,且
点,且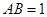 ,
,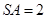 .
.
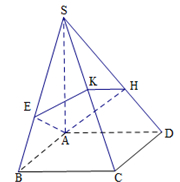
(1)设点 是
是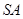 上任一点,试求
上任一点,试求 的最小值;
的最小值;
(2)求证: 、
、 在以
在以 为直径的圆上;
为直径的圆上;
(3)求平面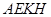 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
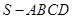 的底面是正方形,侧棱
的底面是正方形,侧棱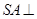 底面
底面 ,过
,过 作
作 垂直
垂直 交
交 于
于 点,作
点,作 垂直
垂直 交
交 于
于 点,平面
点,平面 交
交 于
于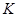 点,且
点,且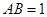 ,
,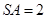 .
.
(1)设点
 是
是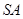 上任一点,试求
上任一点,试求 的最小值;
的最小值;(2)求证:
 、
、 在以
在以 为直径的圆上;
为直径的圆上;(3)求平面
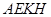 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.(1)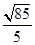 ;(2)详见解析;(3)
;(2)详见解析;(3)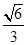 .
.
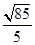 ;(2)详见解析;(3)
;(2)详见解析;(3)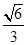 .
.试题分析:(1)将侧面
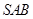 和侧面
和侧面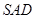 沿着
沿着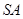 展开至同一平面上,利用
展开至同一平面上,利用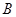 、
、 、
、 三点共线结合余弦定理求出
三点共线结合余弦定理求出 的最小值,即线段
的最小值,即线段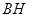 的长度;(2)证
的长度;(2)证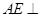 平面
平面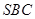 ,从而得到
,从而得到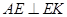 ,同理得到
,同理得到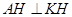 ,进而证明
,进而证明 、
、 在以
在以 为直径的圆上;(3)方法一是建立以点
为直径的圆上;(3)方法一是建立以点 为坐标原点,分别以
为坐标原点,分别以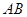 、
、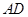 、
、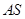 所在的直线为
所在的直线为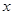 、
、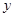 、
、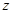 轴的空间直角坐标系,利用空间向量法求平面
轴的空间直角坐标系,利用空间向量法求平面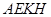 与平面
与平面 所成的锐二面角的余弦值;方法二是延长
所成的锐二面角的余弦值;方法二是延长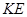 与
与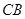 使得它们相交,找出二面角的棱,然后利用三垂线法找出平面
使得它们相交,找出二面角的棱,然后利用三垂线法找出平面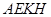 与平面
与平面 所成的锐二面角的平面角,利用直角三角函数来求相应角的余弦值.
所成的锐二面角的平面角,利用直角三角函数来求相应角的余弦值.试题解析:(1)将侧面
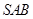 绕侧棱
绕侧棱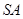 旋转到与侧面
旋转到与侧面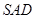 在同一平面内,如下图示,
在同一平面内,如下图示,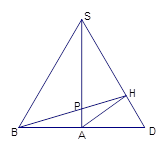
则当
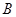 、
、 、
、 三点共线时,
三点共线时, 取最小值,这时,
取最小值,这时, 的最小值即线段
的最小值即线段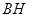 的长,
的长, 设
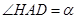 ,则
,则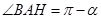 ,
,在
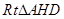 中,
中,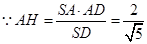 ,
,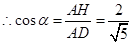 ,
,在三角形
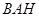 中,有余弦定理得:
中,有余弦定理得: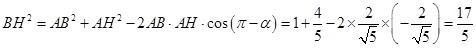 ,
,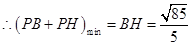 ,
,(2)
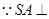 底面
底面 ,
,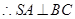 ,又
,又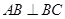
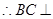 平面
平面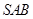 ,又
,又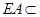 平面
平面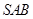 ,
,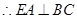 ,
,又
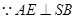 ,
,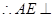 平面
平面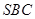 ,
,又
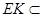 平面
平面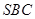 ,
,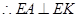 ,
, 同理
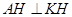 ,
, 、
、 在以
在以 为直径的圆上;
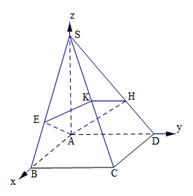
为直径的圆上; (3)方法一:如图,以
 为原点,分别以
为原点,分别以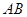 、
、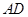 、
、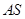 所在的直线为
所在的直线为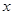 、
、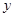 、
、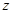 轴,建立空间直角坐标系如下图示,则
轴,建立空间直角坐标系如下图示,则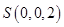 ,
,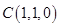 ,由(1)可得
,由(1)可得 ,
, ,
, 平面
平面 ,
,
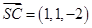 为平面
为平面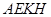 的一个法向量,
的一个法向量,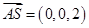 为平面
为平面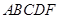 的一个法向量,
的一个法向量,设平面
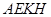 与平面
与平面 所成的锐二面角的平面角为
所成的锐二面角的平面角为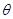 ,
,则
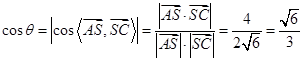 ,
,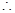 平面
平面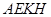 与平面
与平面 所成的锐二面角的余弦值
所成的锐二面角的余弦值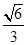 ;
;方法二: 由
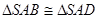 可知
可知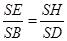 ,故
,故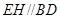 ,
,又
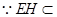 面
面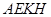 ,
,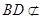 面
面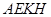 ,
,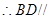 面
面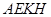 ,
, 设平面
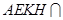 平面
平面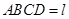 ,
,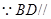 平面
平面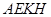 ,
,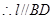 ,
, ,
,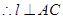 ,
, 又
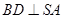 ,
,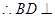 平面
平面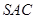 ,又
,又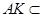 平面
平面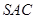 ,
,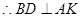 ,
,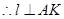 ,
,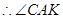 为平面
为平面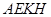 与平面
与平面 所成的锐二面角的一个平面角,
所成的锐二面角的一个平面角, 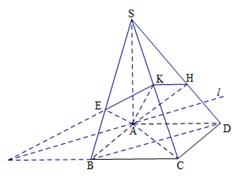
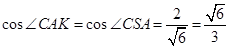 ,
, 平面
平面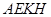 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为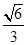 .
.
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
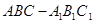 中,
中,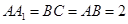 ,
,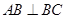 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。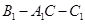 的大小。
的大小。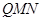 ⊥平面
⊥平面 ,
,  的长度。
的长度。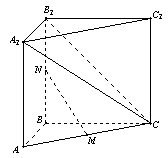
 中,
中, ,
, 是棱
是棱 的中点.如图所示.
的中点.如图所示.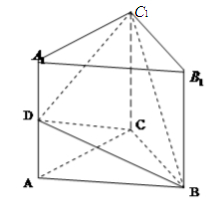
 平面
平面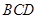 ;
;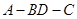 的大小.
的大小.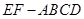 中,
中,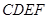 为边长为
为边长为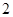 的正方形,
的正方形,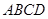 为直角梯形,
为直角梯形,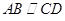 ,
, ,
,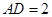 ,
,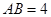 ,
,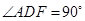 .
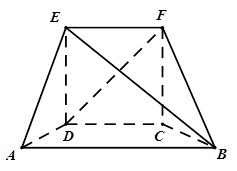
.
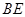 和
和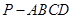 的底面为正方形,侧面
的底面为正方形,侧面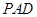
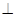 底面
底面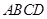 .
.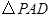 为等腰直角三角形,且
为等腰直角三角形,且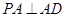 .
.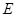 ,
,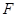 分别为底边
分别为底边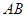 和侧棱
和侧棱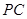 的中点.
的中点.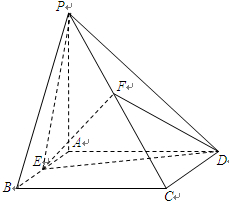
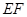 ∥平面
∥平面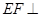 平面
平面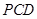 ;
; 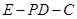 的余弦值.
的余弦值.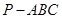 中,
中,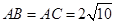 ,
, ,
,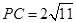 ,点
,点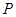 在平面
在平面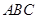 内的射影恰为
内的射影恰为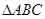 的重心
的重心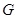 ,M为侧棱
,M为侧棱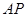 上一动点.
上一动点.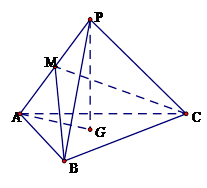
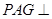 平面
平面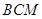 ;
;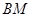 与平面
与平面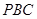 所成角的正弦值.
所成角的正弦值. AB,E是SA的中点.
AB,E是SA的中点.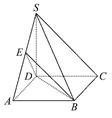
 中,P是侧棱
中,P是侧棱 上的一点,
上的一点,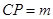 .
. 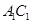 上是否存在一个定点
上是否存在一个定点 ,使得对任意的m,
,使得对任意的m,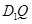 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 
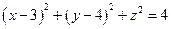 ,则
,则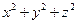 的最小值是( )
的最小值是( )