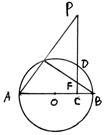
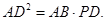题目内容
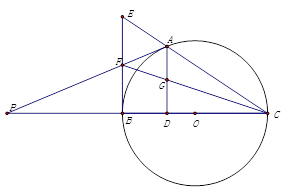
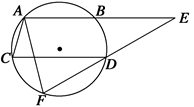
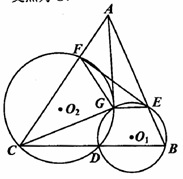
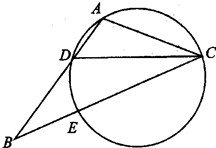
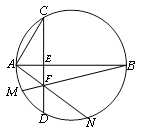
如图,点 是以线段
是以线段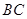 为直径的圆
为直径的圆 上一点,
上一点,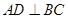 于点
于点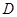 ,过点
,过点 作圆
作圆 的切线,与
的切线,与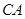 的延长线交于点
的延长线交于点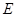 ,点
,点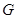 是
是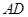 的中点,连结
的中点,连结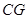 并延长与
并延长与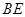 相交于点
相交于点 ,延长
,延长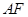 与
与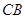 的延长线相交于点
的延长线相交于点 .
.
(Ⅰ)求证: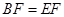 ;
;
(Ⅱ)求证: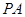 是圆
是圆 的切线.
的切线.
(Ⅰ)详见试题解析;(Ⅱ)详见试题解析.
解析试题分析:(Ⅰ)由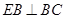 ,
,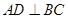 可得
可得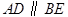 ,从而可得
,从而可得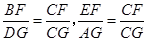
通过等量代换及题设“点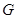 是
是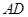 的中点”可得
的中点”可得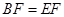 .
.
(Ⅱ)目标是要证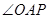 是直角,连结
是直角,连结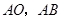 便可看出只要证得
便可看出只要证得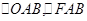 是等腰三角形即可.
是等腰三角形即可.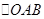 显然是等腰三角形。因为直径上的圆周角是直角,
显然是等腰三角形。因为直径上的圆周角是直角,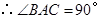 ,所以
,所以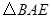 是直角三角形. 由(Ⅰ)得
是直角三角形. 由(Ⅰ)得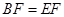 所以
所以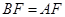 ,从而本题得证.
,从而本题得证.
试题解析:证明:(Ⅰ) 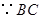 是圆
是圆 的直径,
的直径,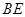 是圆
是圆 的切线,
的切线,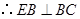 .又
.又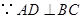 ,
,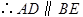 .
.
可以得知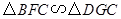 ,
,  .
.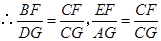 .
.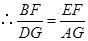 .
.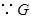 是
是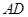 的中点,
的中点,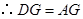 .
.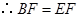 . 5分
. 5分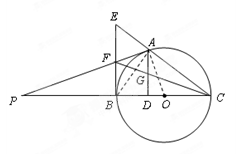
(Ⅱ)连结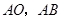 .
.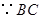 是圆
是圆 的直径,
的直径,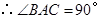 .
.
在 中,由(Ⅰ)得知
中,由(Ⅰ)得知 是斜边
是斜边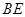 的中点,
的中点,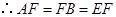 .
.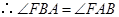 .
.
又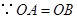 ,
,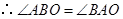 .
.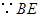 是圆
是圆 的切线,
的切线,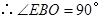
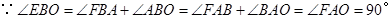 ,
,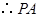 是圆
是圆 的切线. 10分
的切线. 10分
考点:1、相似三角形;2、圆的性质;3、等量代换;4、直角三角形斜边上的中线;5、几何证明

练习册系列答案
相关题目
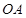 、
、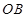 是圆
是圆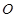 的半径,且
的半径,且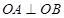 ,
,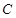 是半径
是半径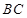 交圆
交圆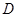 ,过
,过 .求证:
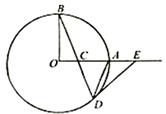
.求证: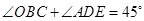 .
.
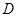 为
为 的
的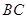 边上一点,
边上一点,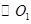 经过点
经过点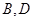 ,交
,交 于另一点
于另一点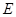 ,
,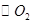 经过点
经过点 ,
,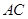 于另一点
于另一点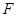 ,
,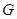 .
.
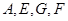 四点共圆;
四点共圆;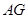 切
切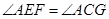 .
.
 切⊙
切⊙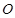 于点E,割线PBA交⊙
于点E,割线PBA交⊙
 ; (Ⅱ)
; (Ⅱ)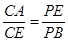 .
. 是
是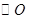 的直径,弦
的直径,弦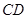 与
与 ,点
,点 为弦
为弦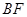 、
、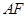 并延长交
并延长交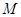 、
、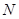 .
.  、
、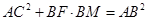 .
.
 是圆的内接四边形,
是圆的内接四边形,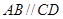 ,过
,过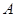 点的圆的切线与
点的圆的切线与 的延长线交于
的延长线交于 点,证明:
点,证明: