题目内容
定义y=log1+xf(x,y),f(x,y)=(1+x)y(x>0,y>0)(1)比较f(1,3)与f(2,2)的大小;
(2)若e<x<y,证明:f(x-1,y)>f(y-1,x);
(3)设g(x)=f(1,log2(x3+ax2+bx+1))的图象为曲线C,曲线C在x处的切线斜率为k,若x∈(1,1-a),且存在实数b,使得k=-4,求实数a的取值范围.
【答案】分析:(1)、由定义知f(x,y)=(1+x)y(x>0,y>0),分别求出f(1,3)与f(2,2)的值后再进行比较.
(2)、要证f(x-1,y)>f(y-1,x),只要证xy>yx即可.
(3)、由题意知:g(x)=x3+ax2+bx+1,且g'(x)=k,于是有3x2+2ax+b=-4在x∈(1,1-a)上有解.又由定义知log2(x3+ax2+bx+1)>0即x3+ax2+bx>0.然后再分类讨论,求出实数a的取值范围.
解答:解:(1)由定义知f(x,y)=(1+x)y(x>0,y>0)
∴f(1,3)=(1+1)3=8,f(2,2)2=9∴f(1,3)<f(2,2).
(2)f(x-1,y)=xy,f(y-1,x)=yx
要证f(x-1,y)>f(y-1,x),只要证xy>yx
∵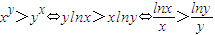
令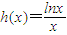 ,则
,则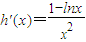 ,当x>e时,h'(x)<0
,当x>e时,h'(x)<0
∴h(x)在(e,+∞)上单调递减.
∵e<x<y∴h(x)>h(y)即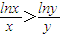
∴不等式f(x-1,y)>f(y-1,x)成立.
(3)由题意知:g(x)=x3+ax2+bx+1,且g'(x)=k
于是有3x2+2ax+b=-4在x∈(1,1-a)上有解.
又由定义知log2(x3+ax2+bx+1)>0即x3+ax2+bx>0
∵x>1∴x2+ax>-b
∴x2+ax>3x2+2ax+4即ax<-2(x2+2)
∴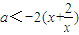 在x∈(1,1-a)有解.
在x∈(1,1-a)有解.
设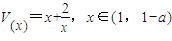
①当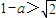 即
即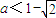 时,
时,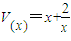 ≥
≥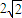 .
.
当且仅当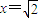 时,
时,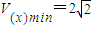
∴当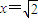 时,
时,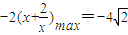 ∴
∴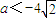 .
.
②当1<1-a≤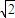 时,即
时,即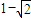 ≤a<0时,
≤a<0时,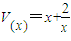 在x∈(1,1-a)上递减,
在x∈(1,1-a)上递减,
∴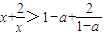 .∴
.∴ 整理得:a2-3a+6<0,无解.
整理得:a2-3a+6<0,无解.
综上所述,实数a的取值范围为 .
.
点评:本题是对数函数的综合题,在解题过程中除正确运用对数的图象和性质,还要充分考虑函数的单调性和导数的几何意义.
(2)、要证f(x-1,y)>f(y-1,x),只要证xy>yx即可.
(3)、由题意知:g(x)=x3+ax2+bx+1,且g'(x)=k,于是有3x2+2ax+b=-4在x∈(1,1-a)上有解.又由定义知log2(x3+ax2+bx+1)>0即x3+ax2+bx>0.然后再分类讨论,求出实数a的取值范围.
解答:解:(1)由定义知f(x,y)=(1+x)y(x>0,y>0)
∴f(1,3)=(1+1)3=8,f(2,2)2=9∴f(1,3)<f(2,2).
(2)f(x-1,y)=xy,f(y-1,x)=yx
要证f(x-1,y)>f(y-1,x),只要证xy>yx
∵
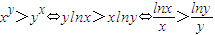
令
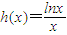 ,则
,则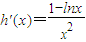 ,当x>e时,h'(x)<0
,当x>e时,h'(x)<0∴h(x)在(e,+∞)上单调递减.
∵e<x<y∴h(x)>h(y)即
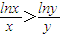
∴不等式f(x-1,y)>f(y-1,x)成立.
(3)由题意知:g(x)=x3+ax2+bx+1,且g'(x)=k
于是有3x2+2ax+b=-4在x∈(1,1-a)上有解.
又由定义知log2(x3+ax2+bx+1)>0即x3+ax2+bx>0
∵x>1∴x2+ax>-b
∴x2+ax>3x2+2ax+4即ax<-2(x2+2)
∴
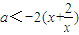 在x∈(1,1-a)有解.
在x∈(1,1-a)有解.设
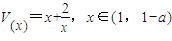
①当
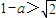 即
即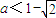 时,
时,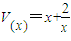 ≥
≥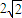 .
.当且仅当
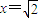 时,
时,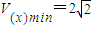
∴当
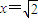 时,
时,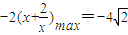 ∴
∴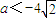 .
.②当1<1-a≤
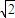 时,即
时,即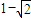 ≤a<0时,
≤a<0时,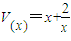 在x∈(1,1-a)上递减,
在x∈(1,1-a)上递减,∴
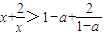 .∴
.∴ 整理得:a2-3a+6<0,无解.
整理得:a2-3a+6<0,无解.综上所述,实数a的取值范围为
 .
.点评:本题是对数函数的综合题,在解题过程中除正确运用对数的图象和性质,还要充分考虑函数的单调性和导数的几何意义.

练习册系列答案
相关题目