题目内容
12.已知cos(α+$\frac{π}{6}$)-sinα=$\frac{4\sqrt{3}}{5}$,则sin(α+$\frac{11π}{6}$)=-$\frac{4}{5}$.分析 由条件利用两角和差的三角公式求得 cos(α+$\frac{π}{3}$)的值,再利用诱导公式求得sin(α+$\frac{11π}{6}$)的值.
解答 解:∵cos(α+$\frac{π}{6}$)-sinα=$\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα-sinα=$\sqrt{3}$($\frac{1}{2}$cosα-$\frac{\sqrt{3}}{2}$sinα)=$\sqrt{3}$cos(α+$\frac{π}{3}$)=$\frac{4\sqrt{3}}{5}$,
∴cos(α+$\frac{π}{3}$)=$\frac{4}{5}$.
则sin(α+$\frac{11π}{6}$)=sin(α-$\frac{π}{6}$)=-cos(α-$\frac{π}{6}$+$\frac{π}{2}$)=-cos(α+$\frac{π}{3}$)=-$\frac{4}{5}$,
故答案为:-$\frac{4}{5}$.
点评 本题主要考查两角和差的三角公式、诱导公式的应用,属于基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
2.若x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$,则z=2x+y的最大值是( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | 4 | D. | 5 |
3.已知实数a1,a2,a3,a4,a5构成等比数列,其中a1=2,a5=32,则公比q的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 4 |
20.设$f(n)={({\frac{1+i}{1-i}})^n}+{({\frac{1-i}{1+i}})^n}$(n∈N),则集合{x|x=f(n)}中元素个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 无穷多个 |
7.某校有一个班级,设变量x是该班同学的姓名,变量y是该班同学的学号,变量z是该班同学的身高,变量w是该班同学某一门课程的考试成绩,则下列选项中一定正确的是(( )
| A. | y是x的函数 | B. | z是y的函数 | C. | w是z的函数 | D. | w是x的函数 |
3.某工程的工作明细表如下:则完成这项工程的最短工期为9天.
| 工作代码 | 紧前工作 | 紧后工作 | 工期/天 |
| A | B、E | --- | 1 |
| B | C | A | 5 |
| C | --- | B、D | 3 |
| D | C | E | 2 |
| E | D | A | 1 |
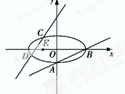 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )