Question

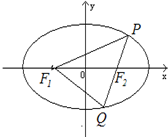（2012•张掖模拟）已知椭圆C：

x2

a2

+

y2

b2

=1的左、右焦点分别为F₁，F₂，它的一条准线为x=4，过点F₂的直线与椭圆C交于P、Q两点．当PQ与x轴垂直时，tan∠F1PF2=

4

3

．
（1）求椭圆C的方程；
（2）若

PF2

=λ•

F2Q

，求△PF₁Q的内切圆面积最大时正实数λ的值．

Answer 1

分析：（1）根据当PQ与x轴垂直时，tan∠F1PF2=

4

3

，可得tan∠F1PF2=

2c

b2 a

=

4

3

，从而可得a=2c，利用椭圆的一条准线为x=4，可得

a2

c

=4，从而可求椭圆C的方程；
（2）分类讨论：①当PQ与x轴垂直时，由S△F1MF2=

1

2

|PQ||F1F2|=

1

2

(|PF1|+|QF1|+|PQ|)r（其中r为△PF₁Q的内切圆半径），可得λ的值；②当PQ与x轴不垂直时，不妨设直线PQ的方程为y=k（x-1）代入椭圆方程，利用韦达定理及S△F1MF2=

1

2

|PQ|d=

1

2

(|PF1|+|QF1|+|PQ|)r，可得结论．

解答：解：（1）∵当PQ与x轴垂直时，tan∠F1PF2=

4

3

∴tan∠F1PF2=

2c

b2 a

=

4

3

∴

ac

b2

=

2

3

，∴a=2c（2分）
∵椭圆的一条准线为x=4
∴

a2

c

=4
∴c=1，a=2，b=

3

故所求椭圆C的方程为

x2

4

+

y2

3

=1．（2分）
（2）由点F₁（-1，0），F₂（1，0），可设P（x₁，y₁），Q（x₂，y₂）
①当PQ与x轴垂直时，根据S△F1MF2=

1

2

•|PQ|•|F1F2|=

1

2

•(|PF1|+|QF1|+|PQ|)•r（其中r为△PF₁Q的内切圆半径），可得|PQ|•2c=4a•r，∴r=

2b2 a •2c

4a

=

3

4

，此时可知λ=1（2分）
②当PQ与x轴不垂直时，不妨设直线PQ的方程为y=k（x-1）代入

x2

4

+

y2

3

=1得（3+4k²）x²-8k²x+4k²-12=0
则

△=144(k2+1)＞0 x1+x2= 8k2 3+4k2 x•x= 4k2-12 3+4k2

（2分）

从而可得|PQ|=

1+k2

•

12 k2+1

3+4k2

=

12(k2+1)

3+4k2

又点F₁（-1，0）到直线PQ的距离d=

|2k|

1+k2

．
依S△F1MF2=

1

2

•|PQ|•d=

1

2

•(|PF1|+|QF1|+|PQ|)•r（其中r为△PF₁Q的内切圆半径）
即|PQ|•d=4a•r（2分）
得r=

|PQ|•d

8

=

1

8

•

12(k2+1)

3+4k2

•

|2k|

1+k2

=3•

k4+k2 16k4+24k2+9

=3•

1 16+ 8 k2 + 1 k4+k2

可知在区间（0，+∞）上该函数单调递增，故当k²→+∞时，即直线PQ的斜率不存在时，r最大为

3

4

，亦即△PF₁Q的内切圆面积最大，此时可知λ=1
综上所求为λ=1．（2分）

点评：本题考查椭圆的标准方程与几何性质，考查分类讨论的数学思想，解题的关键是求出△PF₁Q的内切圆面积，从而确定r最大值．