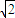题目内容
已知点F、A分别为双曲C：
-
=1(a＞0，b＞0)的左焦点、右顶点，点B（0，b）满足
•
=0，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| FB |
| AB |
A．
| B．
| C．
| D．
|
∵
•
=0
∴FB⊥AB
∴|FB|2+|AB|2=|FA|2，
即c2+b2+a2+b2=（a+c）2，整理得c2-a2-ac=0，等式除以a2得
e2-e-1=0
求得e=
（舍负）
∴e=
故选D
| FB |
| AB |
∴FB⊥AB
∴|FB|2+|AB|2=|FA|2，
即c2+b2+a2+b2=（a+c）2，整理得c2-a2-ac=0，等式除以a2得
e2-e-1=0
求得e=
1±
| ||
| 2 |
∴e=
1+
| ||
| 2 |
故选D
练习册系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
已知点F、A分别为双曲C：
-
=1(a＞0，b＞0)的左焦点、右顶点，点B（0，b）满足
•
=0，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| FB |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
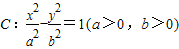的左焦点、右顶点，点B（0，b）满足
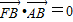，则双曲线的离心率为（ ）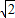
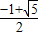
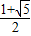
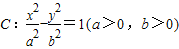的左焦点、右顶点，点B（0，b）满足
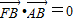，则双曲线的离心率为（ ）
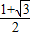
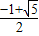
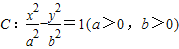的左焦点、右顶点，点B（0，b）满足
，则双曲线的离心率为（ ）
的左焦点、右顶点，点B（0，b）满足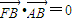
，则双曲线的离心率为（ ）
