题目内容
对于每个实数x,设f(x)取y=2x-1,y=-2x+3两个函数中的最小值,则f(x)的最大值是 .
【答案】分析:在同一坐标系中分别做出函数y=2x-1,y=-2x+3两个函数图象,结合f(x)取y=2x-1,y=-2x+3两个函数中的最小值,得到函数f(x)的图象,数形结合易得答案.
解答:解:∵f(x)取y=2x-1,y=-2x+3两个函数中的最小值,
故函数f(x)的图象如图中红色线条所示:
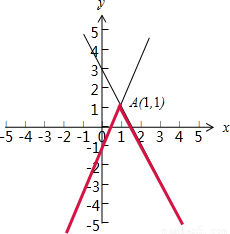
由图易得f(x)的最大值是1
故答案为:1
点评:本题考查的知识点是分段函数及其图象的作法,函数的最值,其中画出函数图象是解答的关键.
解答:解:∵f(x)取y=2x-1,y=-2x+3两个函数中的最小值,
故函数f(x)的图象如图中红色线条所示:
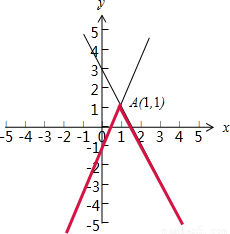
由图易得f(x)的最大值是1
故答案为:1
点评:本题考查的知识点是分段函数及其图象的作法,函数的最值,其中画出函数图象是解答的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目