题目内容
对于每个实数x，设f（x）取y=x2-3x+2，y=x-1，y=5-x三个函数中的最小值，则f（x）的最大值是（ ）
分析：在同一个坐标系中，作出函数y=x2-3x+2，y=x-1，y=5-x的图象，可得函数f（x）的图象（如图红色曲线），数形结合可得f（x）的最大值．
解答：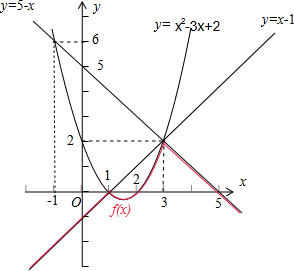
解：在同一个坐标系中，作出函数y=x2-3x+2，y=x-1，y=5-x的图象，
可得函数f（x）的图象（如图红色曲线）所示：
数形结合可得 当x=3时，函数f（x）取得最大值为 2，
故选D．
解：在同一个坐标系中，作出函数y=x2-3x+2，y=x-1，y=5-x的图象，可得函数f（x）的图象（如图红色曲线）所示：
数形结合可得 当x=3时，函数f（x）取得最大值为 2，
故选D．
点评：本题主要考查函数的图象，求函数的最值，体现了转化、数形结合的数学思想，属于基础题．
练习册系列答案
初中暑期衔接系列答案
相关题目