Question

对于每个实数x，设f（x）取y=4x+1，y=x+2，y=-2x+4三个函数中的最小值，用分段函数写出f（x）的解析式，并求f（x）的最大值．

Answer 1

分析：先在同一直角坐标系中画出三条直线，再在不同区间上取靠下的函数图象，组成f（x）的图象，由图象即可看出函数的最大值，通过解直线方程即可得此最值．

解答：解：在同一坐标系下作出三个函数的图象，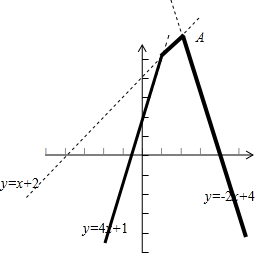
知f（x）=

4x+1，x＜ 1 3 x+2， 1 3 ≤x＜ 2 3 -2x+4，x≥ 2 3

，
由

y=-2x+4 y=x+2

得A（

2

3

，

8

3

），
∴f（x）的最大值为

8

3

．

点评：本题主要考查了利用函数图象数形结合求函数最值的方法，理解新定义函数的意义，并能画出其图象是解决问题的关键．