题目内容
已知点A在圆C：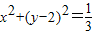
上运动，点B在以
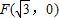为右焦点的椭圆x2+4y2=4上运动，求|AB|的最大值 ．
【答案】分析：先判断出当|BC|最大值时，|AB|取最大值．转化成求|BC|最大值，设B（x，y），利用两点距离公式建立函数模型，利用函数知识求最大值．
解答：解：∵|AB|≤|BC|+|CA|=|BC|+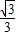
，当且仅当B，C，A共线时取等号．
因此当|BC|最大值时，|AB|取最大值时．
设B（x，y），则 d2=|BC|2=x2+（y-2）2=4（1-y2）+（y-2）2=-3y2-4y+8=-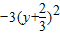
+
，
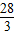∵-1≤y≤1，∴当y=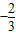
时，d2最大值为
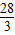，d最大值为
，
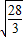|AB|的最大值为
故答案为：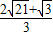
点评：本题考查圆锥曲线简单几何性质，距离的计算，点与圆的位置关系．考查分析解决问题，转化、计算能力．
解答：解：∵|AB|≤|BC|+|CA|=|BC|+
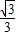，当且仅当B，C，A共线时取等号．因此当|BC|最大值时，|AB|取最大值时．
设B（x，y），则 d2=|BC|2=x2+（y-2）2=4（1-y2）+（y-2）2=-3y2-4y+8=-
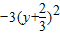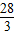+，∵-1≤y≤1，∴当y=
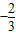时，d2最大值为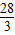，d最大值为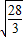，|AB|的最大值为
故答案为：
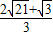
点评：本题考查圆锥曲线简单几何性质，距离的计算，点与圆的位置关系．考查分析解决问题，转化、计算能力．
练习册系列答案
阅读快车系列答案
相关题目
+y2=1上移动,则|PQ|的最大值是( )