题目内容
下列命题错误的是（ ）
分析：对于A命题可转化为如图四面体ABCD，若AB⊥CD，AC⊥BD，则BC⊥AD．后利用几何向量法可判断A，对于B命题转化为在三棱锥A-BCD中，AB、AC、AD两两垂直，点A在平面BCD的射影为H，则点H为△BCD的垂心．然后由线面垂直的性质定理可判断B，利用勾股定理和外心、内心的定义可判断C、D．
解答：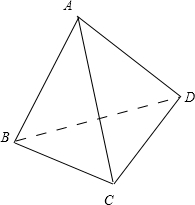
解：A 该命题可转化为如图四面体ABCD，若AB⊥CD，AC⊥BD，则BC⊥AD．
∵AB⊥CD，∴
•
=0，同理
•
=0
∴
•
=(
+
)(
+
)=
•
+
•
+
•
+
•
=
(
+
+
)=
•
=0即BC⊥AD，所以该命题正确．
B该命题转化为在三棱锥A-BCD中，AB、AC、AD两两垂直，点A在平面BCD的射影为H，则点H为△BCD的垂心．
∵BA⊥AC，BA⊥AD，∴BA⊥面ACD，又CD?面ACD，∴BA⊥CD，由三垂线定理及逆定理可知BH⊥CD．
同理 CH⊥BD，DH⊥BC 即点H是△BCD的垂心，所以该命题正确．
C 由题得该点在平面ABC内的射影到到三顶点的距离相等，即为△ABC的外心，所以该命题正确．
D 由题得该点在平面ABC内的射影到到三边的距离相等，而到三角形三边距离相等的点是三角形的内心或是旁心．所以该命题不正确．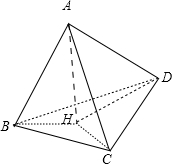
故选D．
解：A 该命题可转化为如图四面体ABCD，若AB⊥CD，AC⊥BD，则BC⊥AD．∵AB⊥CD，∴
| AB |
| CD |
| AC |
| BD |
∴
| BC |
| AD |
| BA |
| AC |
| AB |
| BD |
| BA |
| AB |
| BA |
| BD |
| AC |
| AB |
| AC |
| BD |
=
| BA |
| AB |
| BD |
| CA |
| BA |
| CD |
B该命题转化为在三棱锥A-BCD中，AB、AC、AD两两垂直，点A在平面BCD的射影为H，则点H为△BCD的垂心．
∵BA⊥AC，BA⊥AD，∴BA⊥面ACD，又CD?面ACD，∴BA⊥CD，由三垂线定理及逆定理可知BH⊥CD．
同理 CH⊥BD，DH⊥BC 即点H是△BCD的垂心，所以该命题正确．
C 由题得该点在平面ABC内的射影到到三顶点的距离相等，即为△ABC的外心，所以该命题正确．
D 由题得该点在平面ABC内的射影到到三边的距离相等，而到三角形三边距离相等的点是三角形的内心或是旁心．所以该命题不正确．
故选D．
点评：此题考查是三角形五心的概念及线线垂直判断，第四个命题的判断是学生的难点，因为旁心和内心都符合到三角形三边距离相等的条件，而在我们的教学过程中只注重内心问题．
练习册系列答案
名校通行证有效作业系列答案
相关题目
下列命题错误的是（ ）
| A、对于等比数列{an}而言，若m+n=p+q，则有am•an=ap•aq | ||||||||||||
B、点(
| ||||||||||||
C、若|
| ||||||||||||
| D、?m∈R，使函数f（x）=x2+mx（x∈R）是偶函数 |