题目内容

已知三条不同的直线a，b，c和两个不同的平面β，γ，下列命题错误的是（　　）
分析：A．由线面垂直的性质定理即可判断；
B．举出反例；
C．利用二平面的法向量垂直，故二平面垂直；
D．同C．
解答：解：A．由线面垂直的性质定理可知：
a⊥γ
b⊥γ
⇒a∥b，因此正确；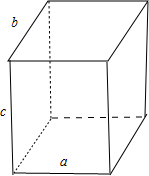
B．如图正方体中：虽然a⊥c，b⊥c，但是a与b异面，
C．∵a⊥γ，b⊥β，∴
a
，
b
分别是平面γ、β的法向量，又
a
⊥
b
，∴γ⊥β，故正确；
D．设平面γ的法向量为
c
，直线a的方向向量为
a
，∵a∥γ，a⊥β，∴
a
⊥
c
，∴γ⊥β，故正确．
综上可知：只有B错误．
故选B．
点评：熟练掌握线线、线面、面面的位置关系是解题的关键．
练习册系列答案
相关题目
已知三条不同的直线a、b、c与平面α,则下列结论不一定正确的是

A.若a⊥α,b⊥α,则a∥b                        B.若a∥b,b∥c,则a∥c

C.若a⊥b,b⊥c,则a∥c                         D.若a⊥α,a∥b,则b⊥α

已知三条不同的直线a、b、c与平面α,则下列结论不一定正确的是

A.若a∥b,b∥c,则a∥c                          B.若a⊥b,b⊥c,则a∥c

C.若a⊥α,b⊥α,则a∥b                          D.若a⊥α,a∥b,则b⊥α

已知三条不同的直线a，b，c和两个不同的平面β，γ，下列命题错误的是（　　）
A．若a⊥γ，b⊥γ，则a∥bB．若a⊥c，b⊥c，则a∥b
C．若a⊥γ，b⊥β，a⊥b，则γ⊥βD．若a∥γ，a⊥β，则γ⊥β
已知三条不同的直线a，b，c和两个不同的平面β，γ，下列命题错误的是（ ）
A．若a⊥γ，b⊥γ，则a∥b
B．若a⊥c，b⊥c，则a∥b
C．若a⊥γ，b⊥β，a⊥b，则γ⊥β
D．若a∥γ，a⊥β，则γ⊥β

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网