题目内容
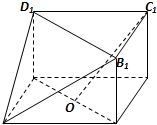 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=2,AD=4,BB1=1.
如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=2,AD=4,BB1=1.设O是线段BD的中点.
(1)求证:C1O∥平面AB1D1;
(2)证明:平面AB1D1⊥平面ADD1.
分析:(1)取B1D1的中点E,连接C1E,OA,易证C1EAO为平行四边形,从而得而C1O∥EA,利用线面平行的判定定理即可;
(2)可根据∠ABC=120°,AB=2,AD=4,证得∠ABD=
,即BD⊥AD,进一步可证BD⊥DD1,从而证得BD⊥平面ADD1,BD∥B1D1,于是得B1D1⊥平面ADD1,利用面面垂直的判定定理可得结论.
(2)可根据∠ABC=120°,AB=2,AD=4,证得∠ABD=
| π |
| 2 |
解答: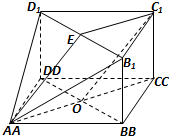 (1)证明:取B1D1的中点E,连接C1E,OA,则A,O,C共线,且C1E=OA,--(1分)
(1)证明:取B1D1的中点E,连接C1E,OA,则A,O,C共线,且C1E=OA,--(1分)
∵BCD-B1C1D1为三棱柱,
∴平面BCD∥平面B1C1D1,
故C1E∥OA,----(3分)
∴C1EAO为平行四边形,
从而C1O∥EA.-----------(5分)
又∵C1O?平面AB1D1,EA?平面AB1D1,
∴C1O∥平面AB1D1.----------(7分)
(2)证明:∵∠ABC=120°,AB=2,AD=4,
∴BD=
=2
,
∴AD2=16=AD2+BD2,∠ABD=
,
即BD⊥AD,----------(10分)
又BB1⊥平面BCD,BD?平面BCD,BB1⊥BD,
在三棱柱BCD-B1C1D1中,BB1∥DD1,则BD⊥DD1,
而DD1∩AD=D,
∴BD⊥平面ADD1,-------(12分)
又BD∥B1D1,得B1D1⊥平面ADD1,
而B1D1?平面AB1D1,
∴平面AB1D1⊥平面ADD1.--------(14分)
 (1)证明:取B1D1的中点E,连接C1E,OA,则A,O,C共线,且C1E=OA,--(1分)
(1)证明:取B1D1的中点E,连接C1E,OA,则A,O,C共线,且C1E=OA,--(1分)∵BCD-B1C1D1为三棱柱,
∴平面BCD∥平面B1C1D1,
故C1E∥OA,----(3分)
∴C1EAO为平行四边形,
从而C1O∥EA.-----------(5分)
又∵C1O?平面AB1D1,EA?平面AB1D1,
∴C1O∥平面AB1D1.----------(7分)
(2)证明:∵∠ABC=120°,AB=2,AD=4,
∴BD=
| 4+16-2×2×4cos600 |
| 3 |
∴AD2=16=AD2+BD2,∠ABD=
| π |
| 2 |
即BD⊥AD,----------(10分)
又BB1⊥平面BCD,BD?平面BCD,BB1⊥BD,
在三棱柱BCD-B1C1D1中,BB1∥DD1,则BD⊥DD1,
而DD1∩AD=D,
∴BD⊥平面ADD1,-------(12分)
又BD∥B1D1,得B1D1⊥平面ADD1,
而B1D1?平面AB1D1,
∴平面AB1D1⊥平面ADD1.--------(14分)
点评:本题考查平面与平面垂直的判定与直线与平面平行的判定,着重考查面面垂直与线面平行的判定定理的应用,注意使用定理的严谨性,属于难题.

练习册系列答案
相关题目
 (2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=
(2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB= ,AD=3,BB1=1.
,AD=3,BB1=1.
 ,AD=3,BB1=1.
,AD=3,BB1=1.
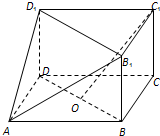 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=
如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB= ,AD=3,BB1=1.
,AD=3,BB1=1.