Question

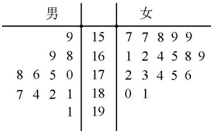某单位为了提高员工素质，举办了一场跳绳比赛，其中男员工12人，女员工18人，其成绩编成如图所示的茎叶图（单位：分），分数在175分以上者定为“运动健将”，并给予特别奖励，其他人员则给予“运动积极分子”称号．
（1）若用分层抽样的方法从“运动健将”和“运动积极分子”中抽取10人，然后再从这10人中选4人，求至少有1人是“运动健将”的概率；
（2）若从所有“运动健将”中选3名代表，用ξ表示所选代表中女“运动健将”的人数，试写出ξ的分布列，并求ξ的数学期望．

Answer 1

分析：（1）根据分层抽样每个人被抽中的概率相等，求出选中的运动健与运动积极分子的人数，利用对立事件的概率公式可求出所求；
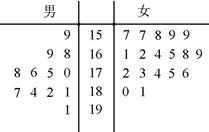
（2）由茎叶图知男“运动健将有”8人，女“运动健将”有4人，故ξ的取值为0，1，2，3，然后根据等可能事件的概率公式求出相应的概率，列出分布列，最后根据数学期望公式解之即可．

解答：解：（1）根据茎叶图，有“运动健将”12人，“运动积极分子”18人------------（1分）
用分层抽样的方法，每个人被抽中的概率为

10

30

=

1

3

，所以选中的运动健将有12×

1

3

=4人，运动积极分子有18×

1

3

=6人-----------------（3分）
设事件A：至少有1名‘运动健将’被选中，则P(A)=1-

C 4 6

C 4 10

=1-

1

14

=

13

14

-----------（5分）
（2）由茎叶图知男“运动健将有”8人，女“运动健将”有4人，故ξ的取值为0，1，2，3------------（7分）
P(ξ=0)=

C 3 8

C 3 12

=

14

55

，P(ξ=1)=

C 2 8 C 1 4

C 3 12

=

28

55

，P(ξ=2)=

C 1 8 C 2 4

C 3 12

=

12

55

，P(ξ=3)=

C 3 4

C 3 12

=

1

55

---（9分）
ξ的分布列为：

ξ	0	1	2	3
P	14 55	28 55	12 55	1 55

---------------（10分）
Eξ=0×

14

55

+1×

28

55

+2×

12

55

+3×

1

55

=1--------------（12分）

点评：本题主要考查了茎叶图、等可能事件的概率以及离散型随机变量的期望，同时考查了运算求解的能力，属于基础题．