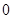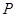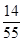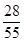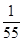��Ŀ����
����С������12�֣�ij��λΪ�����Ա�����ʣ��ٰ���һ������������������Ա��12�ˣ�ŮԱ��18�ˣ���ɼ������ͼ��ʾ�ľ�Ҷͼ����λ���֣���������175�����ϣ���175�֣��߶�Ϊ���˶����������������ر�����������Ա����衰�˶��������ӡ��ƺ�.

�� ���÷ֲ�����ķ����ӡ��˶��������͡��˶��������ӡ��г�ȡ10�ˣ�Ȼ���ٴ���10����ѡ4�ˣ���������1���ǡ��˶��������ĸ��ʣ�
�� �������С��˶���������ѡ3���������� ��ʾ��ѡ������Ů���˶�����������������д��
��ʾ��ѡ������Ů���˶�����������������д�� �ķֲ��У�����
�ķֲ��У����� ����ѧ����.
����ѧ����.
��1��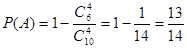 ����2���ֲ���Ϊ��
����2���ֲ���Ϊ��
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
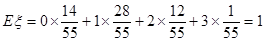
����������������Ҫ�����˾�Ҷͼ����������ã��Լ��ܹ�������������ȡֵ���ֱ�õ����Եĸ���ֵ���õ��ֲ��У����õ�����ֵ��
��1���ȷ�������Ҷͼ���С��˶�������12�ˣ����˶��������ӡ�18�ˣ�Ȼ�����÷ֲ�����ķ����õ�����
��2���ɾ�Ҷͼ֪�С��˶������С�8�ˣ�Ů���˶���������4�ˣ��� ��ȡֵΪ
��ȡֵΪ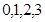 ����ô�����������ĸ��ʹ�ʽ���õ��ֲ��С�
����ô�����������ĸ��ʹ�ʽ���õ��ֲ��С�
�⣺��1�����ݾ�Ҷͼ���С��˶�������12�ˣ����˶��������ӡ�18��------------1��
�÷ֲ�����ķ�����ÿ���˱����еĸ���Ϊ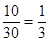 ������ѡ�е��˶�������
������ѡ�е��˶�������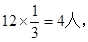
�˶�����������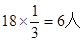 -----------------3��
-----------------3��
���¼�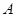 ��������1�����˶���������ѡ�У���
��������1�����˶���������ѡ�У���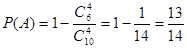
-----------5��
��2���ɾ�Ҷͼ֪�С��˶������С�8�ˣ�Ů���˶���������4�ˣ��� ��ȡֵΪ
��ȡֵΪ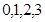
------------7��
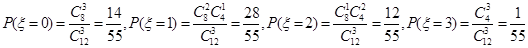 ----------9��
----------9��
 �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
---------------10��
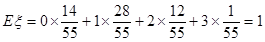 -------------- 12��
-------------- 12��