题目内容
若数列{an}满足
-
=d(n∈N*,d为常数),则称数列{an}为调和数列,已知数列{
}为调和数列,且x1+x2+…+x20=200,则x1+x20=
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| xn |
20
20
;若x5>0,x16>0,则x5•x16的最大值为100
100
.分析:由题意知数列{x}是首相为x1,公差为d1的等差数列,则x1+x2+x3+…+x20=x1+x1+d1+x1+2d1+…+x1+19d1=20x1+(1+19)×
=20d1+190d1=200,所求x5+x16=2x1+19d1=
=20.x1+x20=x5+x16=20.
x5•x16≤(
)2=(
)2=100.
| 19 |
| 2d1 |
| 200 |
| 10 |
x5•x16≤(
| x5+x16 |
| 2 |
| 20 |
| 2 |
解答:解:由题意知数列{an}的倒数成等差数列,则数列{
}的倒数成等差数列,
即x成等差数列,
所以设数列{x}是首相为x1,公差为d1的等差数列,
则x1+x2+x3+…+x20=x1+x1+d1+x1+2d1+…+x1+19d1
=20x1+(1+19)×
=20d1+190d1=200,…①
所求x5+x16=2x1+19d1=
=20.
x1+x20=x5+x16=20.
x5•x16≤(
)2=(
)2=100.
故答案为:20,100.
| 1 |
| x |
即x成等差数列,
所以设数列{x}是首相为x1,公差为d1的等差数列,
则x1+x2+x3+…+x20=x1+x1+d1+x1+2d1+…+x1+19d1
=20x1+(1+19)×
| 19 |
| 2d1 |
所求x5+x16=2x1+19d1=
| 200 |
| 10 |
x1+x20=x5+x16=20.
x5•x16≤(
| x5+x16 |
| 2 |
| 20 |
| 2 |
故答案为:20,100.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
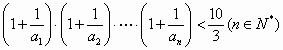
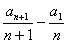 =1,且
=1,且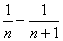 =2(n∈N*),则a10为( )
=2(n∈N*),则a10为( ) =1,且
=1,且 =2(n∈N*),则a3=____________,数列{an}的通项公式为an=____________.
=2(n∈N*),则a3=____________,数列{an}的通项公式为an=____________. =ad-bc,若数列{an}满足
=ad-bc,若数列{an}满足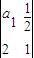 =1,且
=1,且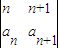 =2(n∈N*)则a3= .数列{an}的通项公式为an= .
=2(n∈N*)则a3= .数列{an}的通项公式为an= . =ad-bc,若数列{an}满足
=ad-bc,若数列{an}满足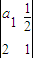 =1,且
=1,且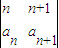 =2(n∈N*)则a3= .数列{an}的通项公式为an= .
=2(n∈N*)则a3= .数列{an}的通项公式为an= .