题目内容
在无穷等比数列{an}中,
(a1+a2+…+an)=
,则首项a1的取值范围是
| lim |
| n→∞ |
| 1 |
| 2 |
(0,
)∪(
,1)
| 1 |
| 2 |
| 1 |
| 2 |
(0,
)∪(
,1)
.| 1 |
| 2 |
| 1 |
| 2 |
分析:无穷等比数列{an}中,
(a1+a2+…+an)=
,推出0<|q|<1,然后求出首项a1的取值范围.
| lim |
| n→∞ |
| 1 |
| 2 |
解答:解:因为无穷等比数列{an}中,
(a1+a2+…+an)=
,所以|q|<1,
=
,所以a1=
(1-q),∵-1<q<1且q≠0
∴0<a1<1且a1≠
故答案为:(0,
)∪(
,1).
| lim |
| n→∞ |
| 1 |
| 2 |
| a1 |
| 1-q |
| 1 |
| 2 |
| 1 |
| 2 |
∴0<a1<1且a1≠
| 1 |
| 2 |
故答案为:(0,
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查无穷等比数列的极限存在条件的应用,解题时要注意极限逆运算的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
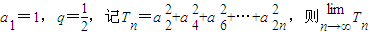 等于 .
等于 .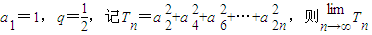 等于 .
等于 .