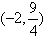题目内容
设f(x)=
，若f（t）＞2，则实数t的取值范围是（ ）
|
分析：当t≥0时，由f（t）=t2-2t-1＞2，解得实数t的取值范围． 当t＜0时，由f（t）=-2t+6＞2，解得实数t的取值范围．再把这两个范围取并集，即得所求．
解答：解：当t≥0时，由f（t）=t2-2t-1＞2，解得 t＜-1，或t＞3，故实数t的取值范围是 （3，+∞）．
当t＜0时，由f（t）=-2t+6＞2，解得 t＜2，故实数t的取值范围是 （-∞，0）．
综上可得，实数t的取值范围是 （-∞，0）∪（3，+∞），
故选D．
当t＜0时，由f（t）=-2t+6＞2，解得 t＜2，故实数t的取值范围是 （-∞，0）．
综上可得，实数t的取值范围是 （-∞，0）∪（3，+∞），
故选D．
点评：本题主要考查二次函数的性质，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
)
，+∞)
,+∞)
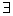x0∈(0，+∞)使得f(x0)≥g(x0)，则实数m的取值范围是
B. 
C. 
D. 