题目内容
【题目】如图,在四棱锥E﹣ABCD中,底面ABCD是矩形,AB=1,AE⊥平面CDE, ![]() ,F为线段DE上的一点.
,F为线段DE上的一点. 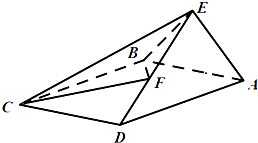
(1)求证:平面AED⊥平面ABCD;
(2)若二面角E﹣BC﹣F与二面角F﹣BC﹣D的大小相等,求DF的长.
【答案】
(1)证明:∵AE⊥面CDE,CD面CDE,
∴AE⊥CD,
又∴ ![]() 是矩形,
是矩形,
∴AD⊥CD,∴CD⊥面AED,
又∵CD面ABCD,
∴平面AED⊥平面ABCD.
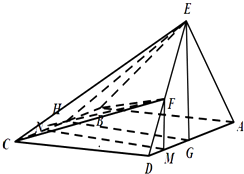
(2)解:取AD,BC的中点G,H,
连结EG,GH,EH,过F作FM||EG交AD于M,
过M作NM||HG交BC于N,连结FN,
∵ ![]() ,∴
,∴ ![]() 且EG⊥AD,
且EG⊥AD,
∵平面AED⊥平面ABCD,∴EG⊥面ABCD,GH⊥BC,
∴EH⊥BC,∴∠EHG就是二面角E﹣BC﹣D的平面角,
同理∠FNM就是二面角F﹣BC﹣D的平面角,
由题意得∠EHG=2∠FNM,
而 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)推导出AE⊥CD,AD⊥CD,从而CD⊥面AED,由此能证明平面AED⊥平面ABCD.(2)取AD,BC的中点G,H,连结EG,GH,EH,过F作FM||EG交AD于M,过M作NM||HG交BC于N,连结FN,推导出∠EHG就是二面角E﹣BC﹣D的平面角,∠FNM就是二面角F﹣BC﹣D的平面角,由此能求出DF的长.
【考点精析】关于本题考查的平面与平面垂直的判定,需要了解一个平面过另一个平面的垂线,则这两个平面垂直才能得出正确答案.

【题目】2016年中国(云南赛区)三对三篮球联赛在昆明市体育局的大力支持下,圆满顺利结束.组织方统计了来自![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队的男子的平均身高与本次比赛的平均得分,如下表所示:
球队 |
|
|
|
|
|
平均身高 | 170 | 174 | 176 | 181 | 179 |
平均得分 | 62 | 64 | 66 | 70 | 68 |
(2)若![]() 队平均身高为
队平均身高为![]()
![]() ,根据(1)中所求得的回归方程,预测
,根据(1)中所求得的回归方程,预测![]() 队的平均得分.(精确到个位)
队的平均得分.(精确到个位)
注:回归方程![]() 中斜率和截距最小二乘估计公式分别为
中斜率和截距最小二乘估计公式分别为
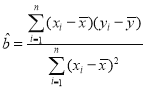 ,
,![]() .
.