题目内容
(本题10分)袋中有红、白两种颜色的小球共7个,它们除颜色外完全相同,从中任取2个,都是白色小球的概率为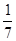 ,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。
,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。
(1)求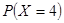 ;
;
(2)求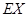 。
。
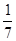 ,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。
,甲、乙两人不放回地从袋中轮流摸取一个小球,甲先取,乙后取,然后再甲取……,直到两人中有一人取到白球时游戏停止,用X表示游戏停止时两人共取小球的个数。(1)求
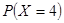 ;
;(2)求
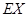 。
。 (1)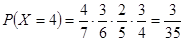 ;
;
(2)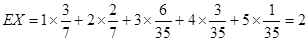 。
。
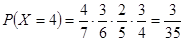 ;
;(2)
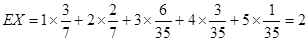 。
。本题考查概率的公式与分布列的计算,注意概率计算是基础,平时要加强概率的计算的训练.
(1)设袋中有玩具“圆圆”n个,根据题意,从中任取2个玩具都是“圆圆”的概率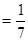
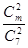
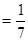 ,解得
,解得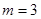 可得。
可得。
(2)由题意可知X的可能取值为1,2,3,4,5;分别求出其概率,由期望的公式,计算可得答案.
解:(1)设白色小球有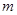 个,则由题设可知,
个,则由题设可知,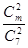
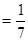 ,解得
,解得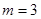 。(2分)
。(2分)
所以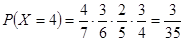 (4分)
(4分)
(2)由题设可知,X的可能取值是1,2,3,4,5
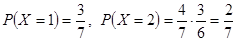 。
。
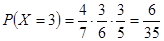 ,
,
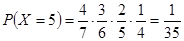 (8分)
(8分)
所以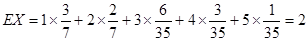 (10分)
(10分)
(1)设袋中有玩具“圆圆”n个,根据题意,从中任取2个玩具都是“圆圆”的概率
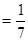
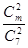
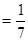 ,解得
,解得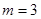 可得。
可得。(2)由题意可知X的可能取值为1,2,3,4,5;分别求出其概率,由期望的公式,计算可得答案.
解:(1)设白色小球有
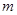 个,则由题设可知,
个,则由题设可知,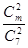
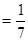 ,解得
,解得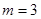 。(2分)
。(2分)所以
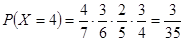 (4分)
(4分)(2)由题设可知,X的可能取值是1,2,3,4,5
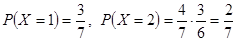 。
。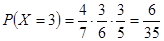 ,
,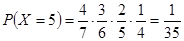 (8分)
(8分)所以
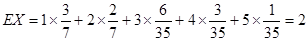 (10分)
(10分)
练习册系列答案
相关题目
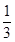 ,将赝品错误地鉴定为正品的概率为
,将赝品错误地鉴定为正品的概率为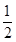 ,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数
,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数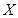 的分布列及数学期望.
的分布列及数学期望. 各局比赛的结果都相互独立,第
各局比赛的结果都相互独立,第 局甲当裁判.
局甲当裁判.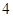 局甲当裁判的概率;
局甲当裁判的概率;
 三个社区中各选一人,求恰好有2人是低碳族的概率;
三个社区中各选一人,求恰好有2人是低碳族的概率; 是一个离散型随机变量,其分布列如下表,试求随机变量
是一个离散型随机变量,其分布列如下表,试求随机变量 与方差
与方差 .
.
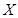 为选出的4名选手中女选手的人数,求
为选出的4名选手中女选手的人数,求



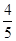
 ,求
,求
