题目内容
一条斜率为1的直线l与离心率为
解:∵e=![]() ,∴b2=2a2.
,∴b2=2a2.
∴双曲线方程可化为2x2-y2=2a2.
设直线方程为y=x+m,
由 得x2-2mx-m2-2a2=0,
得x2-2mx-m2-2a2=0,
∴Δ=4m2+4(m2+2a2)>0.
∴直线一定与双曲线相交.
设P(x1,y1)、Q(x2,y2),则x1+x2=2m,x1x2=-m2-2a2.
∵![]() =3
=3![]() ,xR=
,xR=![]() =0,
=0,
∴x1=-3x2.
∴x2=-m,-3x22=-m2-2a2.
消去x2,得m2=a2.
![]() ·
·![]() =x1x2+y1y2=x1x2+(x1+m)(x2+m)
=x1x2+y1y2=x1x2+(x1+m)(x2+m)
=2x1x2+m(x1+x2)+m2=m2-4a2=-3,
∴m=±1,a2=1,b2=2.
∴直线方程为y=x±1,双曲线方程为x2-![]() =1.
=1.

练习册系列答案
相关题目
 的椭圆C:
的椭圆C: +
+ =1(a>b>0)交于P、Q两点,直线l与y轴交于点R,且
=1(a>b>0)交于P、Q两点,直线l与y轴交于点R,且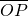 •
•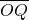 =-3,
=-3, =3
=3 ,求直线l和椭圆C的方程.
,求直线l和椭圆C的方程. 的双曲线
的双曲线 交于P、Q两点,直线l与y轴交于点R,且
交于P、Q两点,直线l与y轴交于点R,且 ,
,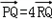 ,求直线与双曲线方程
,求直线与双曲线方程