题目内容
函数f(x)的图象与函数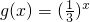 的图象关于直线y=x对称,设φ(x)=f(4x-x2),则函数φ(x)的递减区间是
的图象关于直线y=x对称,设φ(x)=f(4x-x2),则函数φ(x)的递减区间是
- A.(-∞,2]
- B.[2,4)
- C.(0,4)
- D.(0,2]
D
分析:根据函数f(x)的图象与函数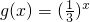 的图象关于直线y=x对称,可得
的图象关于直线y=x对称,可得 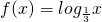 ,可得
,可得 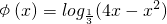 ,先求出该函数的定义域(0,4),然后根据复合函数的单调性可求函数φ(x)的递减区间.
,先求出该函数的定义域(0,4),然后根据复合函数的单调性可求函数φ(x)的递减区间.
解答:∵函数f(x)的图象与函数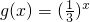 的图象关于直线y=x对称,
的图象关于直线y=x对称,
∴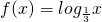
∴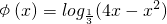
∵4x-x2>0?0<x<4,它的定义域为(0,4)
令t=4x-x2,则t=4x-x2在0(0,2]单调递增,在[2,4)单调递减
而函数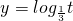 在(0,+∞)单调递减
在(0,+∞)单调递减
从而可知函数φ(x)的单调减区间是:(0,2].
故选D.
点评:本题主要考查了互为反函数的函数的解析式的求解,由对数函数与二次函数复合的函数的单调区间的求解,此类问题的容易出错点是:漏掉对函数定义域的求解,造成单调区间的扩大而错误.
分析:根据函数f(x)的图象与函数
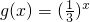 的图象关于直线y=x对称,可得
的图象关于直线y=x对称,可得 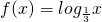 ,可得
,可得 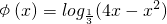 ,先求出该函数的定义域(0,4),然后根据复合函数的单调性可求函数φ(x)的递减区间.
,先求出该函数的定义域(0,4),然后根据复合函数的单调性可求函数φ(x)的递减区间.解答:∵函数f(x)的图象与函数
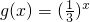 的图象关于直线y=x对称,
的图象关于直线y=x对称,∴
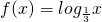
∴
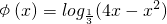
∵4x-x2>0?0<x<4,它的定义域为(0,4)
令t=4x-x2,则t=4x-x2在0(0,2]单调递增,在[2,4)单调递减
而函数
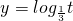 在(0,+∞)单调递减
在(0,+∞)单调递减从而可知函数φ(x)的单调减区间是:(0,2].
故选D.
点评:本题主要考查了互为反函数的函数的解析式的求解,由对数函数与二次函数复合的函数的单调区间的求解,此类问题的容易出错点是:漏掉对函数定义域的求解,造成单调区间的扩大而错误.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目