Question

设函数f（x）=x³-12x，则下列结论正确的是（　　）

A．函数f（x）在（-∞，-1）上单调递增

B．函数f（x）的极小值是-12

C．函数f（x）的图象与直线y=10只有一个公共点

D．函数f（x）的图象在点（-2，f（-2））处的切线方程为y=16

Answer 1

分析：先求出其导函数，利用其导函数画出原函数的大致图象，结合图象即可判断出正确结论．

解答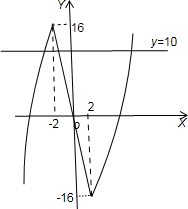：解：因为f（x）=x³-12x，
所以：f′（x）=3x²-12=3（x-2）（x+2）．
由f′（x）＞0⇒x＞2或x＜-2．
f′（x）＜0⇒-2＜x＜2．
∴f（x）在（-∞，-2），（2，+∞）上递增，在（-2，2）上递减．
且f（x）在x=-2处有极大值为：f（-2）=16，在x=2处有极小值为：f（2）=-16．
其大致图象为：
故答案A，B，C错．
故选：D．

点评：本题主要考查学生会利用导数求曲线上过某点切线方程的斜率，会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值．解决此类问题的关键在于会求常见函数的导函数，并知道导函数的应用．