题目内容
已知命题p:实数x满足 ,命题q:实数x满足x2-2x+(1-m2)≤0(m>0),若¬p是¬q的必要不充分条件,求实数m的取值范围.
,命题q:实数x满足x2-2x+(1-m2)≤0(m>0),若¬p是¬q的必要不充分条件,求实数m的取值范围.
【答案】分析:由命题p成立求得x的范围为A,由命题q成立求得x的范围为B,由题意可得A?B,可得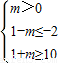 ,由此求得
,由此求得
实数m的取值范围.
解答:解:由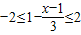 ,解得-2≤x≤10,…(3分)
,解得-2≤x≤10,…(3分)
记A={x|p}={x|-2≤x≤10}.
由x2-2x+(1-m2)≤0(m>0),得 1-m≤x≤1+m.…(6分)
记B={x|1-m≤x≤1+m,m>0},
∵¬p是¬q的必要不充分条件,
∴p是q的充分不必要条件,即 p⇒q,且 q不能推出 p,∴A?B.…(8分)
要使A?B,又m>0,则只需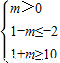 ,…(11分)
,…(11分)
∴m≥9,
故所求实数m的取值范围是[9,+∞).
点评:本题主要考查分式不等式的解法,充分条件、必要条件、充要条件的定义,体现了等价转化的数学思想,
属于中档题.
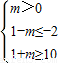 ,由此求得
,由此求得实数m的取值范围.
解答:解:由
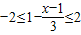 ,解得-2≤x≤10,…(3分)
,解得-2≤x≤10,…(3分)记A={x|p}={x|-2≤x≤10}.
由x2-2x+(1-m2)≤0(m>0),得 1-m≤x≤1+m.…(6分)
记B={x|1-m≤x≤1+m,m>0},
∵¬p是¬q的必要不充分条件,
∴p是q的充分不必要条件,即 p⇒q,且 q不能推出 p,∴A?B.…(8分)
要使A?B,又m>0,则只需
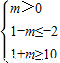 ,…(11分)
,…(11分)∴m≥9,
故所求实数m的取值范围是[9,+∞).
点评:本题主要考查分式不等式的解法,充分条件、必要条件、充要条件的定义,体现了等价转化的数学思想,
属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
已知命题p:实数x满足logax>loga(1-x),其中0<a<1;命题q:实数x满足-1<x<1;则p是q的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分也不必要条件 |