题目内容
设0<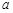 <1,函数
<1,函数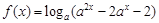 ,则使
,则使 的x的取值范围是
的x的取值范围是
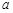 <1,函数
<1,函数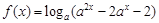 ,则使
,则使 的x的取值范围是
的x的取值范围是A. | B.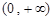 | C. | D. |
C
专题:计算题.
分析:结合对数函数、指数函数的性质和复合函数的单调性可知:当0<a<1,loga(a2x-2ax-2)<0时,有a2x-2ax-2>1,解可得答案.
解答:解:设0<a<1,函数f(x)=loga(a2x-2ax-2),
若f(x)<0
则loga(a2x-2ax-2)<0,∴a2x-2ax-2>1
∴(ax-3)(ax+1)>0∴ax-3>0,∴x<loga3,
故选C.
点评:解题中要注意0<a<1时复合函数的单调性,以避免出现不必要的错误.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足 ,则
,则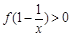 的解是
的解是



 在区间
在区间 上单调递减,实数
上单调递减,实数 的取值范围
的取值范围 )
) )
) ,在函数
,在函数
 的图象上有
的图象上有 、
、 、
、 三点,它们的横坐标分别为
三点,它们的横坐标分别为 、
、 、
、 。
。 的面积为
的面积为 ,求
,求 ;
; ,设
,设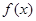 的反函数为
的反函数为 。若关于x的不等式
。若关于x的不等式 有解,则m的取值范围是( )
有解,则m的取值范围是( )



 的定义域。
的定义域。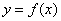 的图象与函数
的图象与函数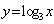 的图象关于直线
的图象关于直线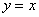 对称,则
对称,则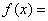 __
__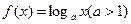 的导函数是
的导函数是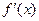 ,记
,记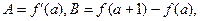
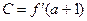 则 ( )
则 ( ) ,则
,则 从大到小的顺序是 ★
从大到小的顺序是 ★