题目内容
设一地球仪的球心为空间直角坐标系的原点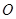 ,球面上有两个点
,球面上有两个点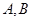 的坐标分别为
的坐标分别为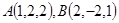 ,则
,则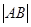 =( )
=( )
| A.18 | B.12 | C.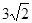 | D.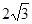 |
C
解析试题分析:由两点间的距离公式,得 。
。
考点:空间中的两点间的距离公式。
点评:直接考查空间中的两点间的距离公式,属于基础题型。

练习册系列答案
相关题目
已知长方体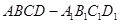 ,下列向量的数量积一定不为
,下列向量的数量积一定不为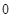 的是 ( )
的是 ( )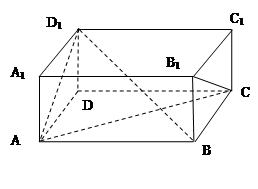
A.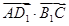 | B. | C.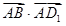 | D.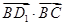 |
已知等差数列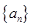 的前n项和为
的前n项和为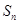 ,且
,且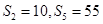 ,则过点
,则过点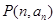 和
和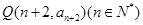 的直线的一个方向向量的坐标可以是( )
的直线的一个方向向量的坐标可以是( )
A.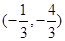 | B.(2,4) | C.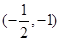 | D.(-1,-1) |
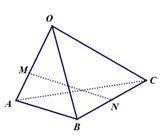
如图,空间四边形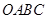 中,
中,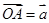 ,
,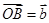 ,
,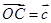 ,点
,点 在线段
在线段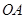 上,且
上,且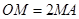 ,点
,点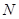 为
为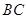 的中点,则
的中点,则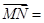 ( )
( )
A.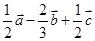 | B. |
C.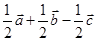 | D.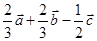 |
已知向量a=(3,5,-1),b=(2,2,3),c=(4,-1,-3),则向量2a-3b+4c的坐标为( )
| A.(16,0,-23) | B.(28,0,-23) |
| C.(16,-4,-1) | D.(0,0,9) |
已知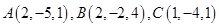 ,则向量
,则向量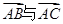 的夹角为 ( )
的夹角为 ( )
| A.30° | B.45° | C.60° | D.90° |
过正方形ABCD的顶点A,引PA⊥平面ABCD.若PA=BA,则平面ABP和平面CDP所成的二面角的大小是( ).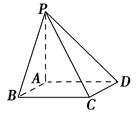
| A.30° | B.45° | C.60° | D.90° |
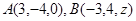 两点间的距离为10,则
两点间的距离为10,则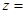 __________.
__________.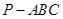 中,
中, 平面
平面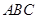 ,
,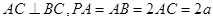 ,则
,则 与平面
与平面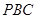 所成角的正弦值为__________.
所成角的正弦值为__________.