题目内容
甲有一只放有x个红球，y个黄球，z个白球的箱子，且x＋y＋z＝6(x，y，z∈N)，乙有一只放有3个红球，2个黄球，1个白球的箱子，两个各自从自己的箱子中任取一球，规定：当两球同色时甲胜，异色时乙胜．
(1)用x、y、z表示甲胜的概率；
(2)若又规定当甲取红、黄、白球而胜的得分分别为1、2、3分，否则得0分，求甲得分的期望的最大值及此时x、y、z的值．
答案：
解析：
解析：
|
(1)P(甲胜)＝P(甲、乙均取红球)＋P(甲、乙均取白球)＋P(甲、乙均取黄球) (2)设甲的得分为随机变量 ∵x、y、z∈N且x＋y＋z＝6，∴0≤y≤6 |
(6分)(用两个字母表示不扣分)
，则：
］
练习册系列答案
一线名师权威作业本系列答案
相关题目
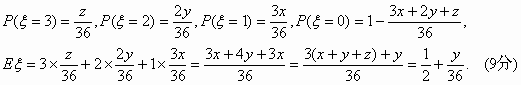
用x、y、z表示甲胜的概率；
时，求y与z；