题目内容
甲有一只放有x个红球,y个黄球,z个白球的箱子,乙有一只放有3个红球,2个黄球,1个白球的箱子,
(1)两个各自从自己的箱子中任取一球,规定:当两球同色时甲胜,异色时乙胜。若 用x、y、z表示甲胜的概率;
用x、y、z表示甲胜的概率;
2)在(1)下又规定当甲取红、黄、白球而胜的得分分别为1、2、3分,否则得0分,求甲得分的期望的最大值及此时x、y、z的值。
【答案】
(1)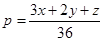 ;(2)
;(2)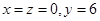 时,
时,
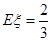 最大.
最大.
【解析】
试题分析:(1)甲胜包含甲、乙均取红球,甲、乙均取白球,甲、乙均取黄球三种情况,将这三种情况的概率求出相加即得.(2)设甲的得分为随机变量 ,根据题设
,根据题设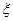 可取0、1、2、3.由(1)可得
可取0、1、2、3.由(1)可得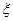 取1、2、3的概率(用x,y,z表示),用1减去这三个概率即得
取1、2、3的概率(用x,y,z表示),用1减去这三个概率即得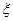 取0的概率,从而可得
取0的概率,从而可得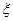 的期望,再根据
的期望,再根据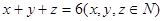 可得期望的最大值及x,y,z的值.
可得期望的最大值及x,y,z的值.
试题解析:(1)P(甲胜)=P(甲、乙均取红球)+P(甲、乙均取白球)+P(甲、乙均取黄球)
(2)设甲的得分为随机变量 ,则:
,则:

∵x、y、z∈N且x+y+z=6,∴0≤y≤6
所以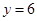 时,
时,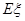 取得最大值
取得最大值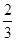 ,此时
,此时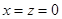 .
.
考点:1、随机变量的分布列及期望;2、最值问题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 时,求y与z;
时,求y与z;