题目内容
设两个非零向量 1与
1与 2不共线
2不共线
①如果 =
= 1+
1+ 2,
2, =2
=2 1+8
1+8 2,
2, =3(
=3( 1-
1- 2)求证:A、B、D三点共线.
2)求证:A、B、D三点共线.
②试确定实数k的值,使k 1+
1+ 2和
2和 1+k
1+k 2共线.
2共线.
解:①证明:∵ =
= =5
=5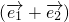 ,而
,而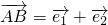 ,∴
,∴ =5
=5 ,∴A、B、D三点共线;
,∴A、B、D三点共线;
②若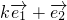 与
与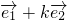 共线,则存在实数λ使得
共线,则存在实数λ使得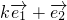 =
=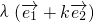 成立,
成立,
∴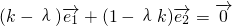 ,
,
∵两个非零向量 与
与 不共线,∴
不共线,∴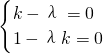 ,解得k=±1.
,解得k=±1.
分析:①只要证明存在实数λ使得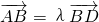 成立即可;
成立即可;
②利用向量共线的充要条件和两个非零向量 与
与 不共线即可求出.
不共线即可求出.
点评:熟练掌握向量共线的充要条件和两个非零向量 与
与 不共线的条件是解题的关键.
不共线的条件是解题的关键.
 =
= =5
=5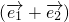 ,而
,而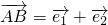 ,∴
,∴ =5
=5 ,∴A、B、D三点共线;
,∴A、B、D三点共线;②若
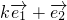 与
与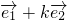 共线,则存在实数λ使得
共线,则存在实数λ使得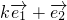 =
=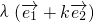 成立,
成立,∴
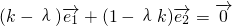 ,
,∵两个非零向量
 与
与 不共线,∴
不共线,∴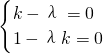 ,解得k=±1.
,解得k=±1.分析:①只要证明存在实数λ使得
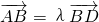 成立即可;
成立即可;②利用向量共线的充要条件和两个非零向量
 与
与 不共线即可求出.
不共线即可求出.点评:熟练掌握向量共线的充要条件和两个非零向量
 与
与 不共线的条件是解题的关键.
不共线的条件是解题的关键. 
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 1与
1与 2不共线
2不共线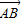 =
=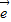 1+
1+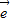 2,
2,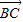 =2
=2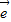 1+8
1+8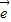 2,
2,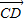 =3(
=3( 1-
1-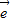 2)求证:A、B、D三点共线.
2)求证:A、B、D三点共线.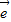 1+
1+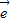 2和
2和 1+k
1+k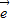 2共线.
2共线.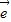 1与
1与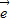 2不共线
2不共线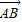 =
=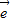 1+
1+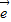 2,
2,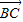 =2
=2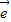 1+8
1+8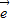 2,
2,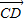 =3(
=3(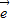 1-
1-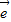 2)求证:A、B、D三点共线.
2)求证:A、B、D三点共线.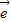 1+
1+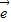 2和
2和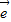 1+k
1+k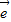 2共线.
2共线.