题目内容
(本小题满分12分)已知直角 的三边长
的三边长 ,满足
,满足
(1)已知 均为正整数,且
均为正整数,且 成等差数列,将满足条件的三角形的面积从小到大排成一列
成等差数列,将满足条件的三角形的面积从小到大排成一列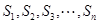 ,且
,且 ,求满足不等式
,求满足不等式 的所有
的所有 的值;
的值;
(2)已知 成等比数列,若数列
成等比数列,若数列 满足
满足 ,证明数列
,证明数列 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且 是正整数.
是正整数.
【答案】
(1) 2、3、4;(2)参考解析
【解析】
试题分析:(1)已知直角三角形中三边是正整数,并且成等差数列.由此可得首项与公差的关系.从而写出三角形的面积的表达式.由于面积是从小到大排的,所以把公差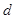 .改成
.改成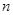 没关系.由于数列
没关系.由于数列 的前
的前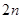 项的和的特点是每项是一项正一项负.所以相邻的两项用平方差公式化简.即可得一个等差数列的求和的式子. 由
项的和的特点是每项是一项正一项负.所以相邻的两项用平方差公式化简.即可得一个等差数列的求和的式子. 由 得
得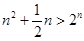 ,由于指数函数是爆炸性的变化,所以要符合该不等式的不是很多,再由
,由于指数函数是爆炸性的变化,所以要符合该不等式的不是很多,再由 .利用二项式定理展开即可得
.利用二项式定理展开即可得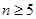 时,
时, .所以
.所以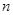 只有2,3,4三种情况.
只有2,3,4三种情况.
(2);因为 成等比数列.解直角三角形三边的关系可求得
成等比数列.解直角三角形三边的关系可求得 .所以可以写出
.所以可以写出 的表达式.在递推一个式子.两式相加,再利用
的表达式.在递推一个式子.两式相加,再利用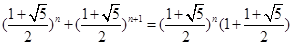 =
= =
=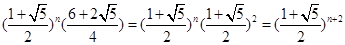 .从而可得
.从而可得 .从而即可得解答结论.再说明前三项符合即可.
.从而即可得解答结论.再说明前三项符合即可.
试题解析:(1)设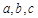 的公差为
的公差为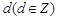 ,则
,则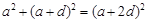
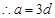
设三角形的三边长为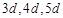 ,面积
,面积 , 2分
, 2分


由 得
得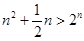 ,
,
当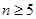 时,
时, ,
,
经检验当 时,
时,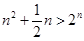 ,当
,当 时,
时,
综上所述,满足不等式 的所有
的所有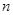 的值为2、3、4 6分
的值为2、3、4 6分
(2)证明因为 成等比数列,
成等比数列, .
.
由于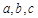 为直角三角形的三边长,知
为直角三角形的三边长,知 ,
, ,
8分
,
8分
又 ,得
,得 ,
,
于是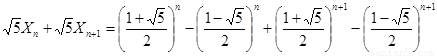
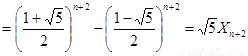
 ,则有
,则有 .
.
故数列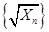 中的任意连续三项为边长均可以构成直角三角形 10分
中的任意连续三项为边长均可以构成直角三角形 10分
因为  ,
,
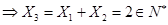 ,由数学归纳法得:
,由数学归纳法得:
由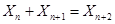 ,同理可得
,同理可得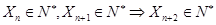 ,
,
故对于任意的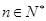 都有
都有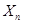 是正整数 12分
是正整数 12分
考点:1.等差数列的中项公式.2.等比数列的中项公式.3.利用平方差公式局部求和.4.数学归纳法.5.数列递推思想.6.含根式的化简.

练习册系列答案
相关题目