题目内容
在将(x2-x-2)4展开的多项式中,x项的系数是 ________.
32
分析:先将式子化简,将展开式中x的系数转化为两个二项式展开式系数的问题;利用二项展开式的通项公式求出两个二项式的通项,求出需要的项的系数,求出展开式中x像的系数.
解答:(x2-x-2)4=(x-2)4(x+1)4
展开的多项式中x项的系数是(x-2)4中的x的系数乘以(x+1)4的常数项加上(x-2)4中的常数项乘以(x+1)4中的x的系数
∵(x-2)4展开式的通项为Tr+1=(-2)rC4rx4-r
令4-r=0得r=4,其常数项为16;令4-r=1得r=3所以其展开式含x的系数为-32
∵(x+1)4展开式的通项为Tk+1=C4kxk
∴展开式的常数项为1;含x的系数为4
∴展开的多项式中,x项的系数是16×4-32=32
故答案为32
点评:本题考查等价转化的思想方法、考查利用二项展开式的通项公式解决二项展开式的特定项问题.
分析:先将式子化简,将展开式中x的系数转化为两个二项式展开式系数的问题;利用二项展开式的通项公式求出两个二项式的通项,求出需要的项的系数,求出展开式中x像的系数.
解答:(x2-x-2)4=(x-2)4(x+1)4
展开的多项式中x项的系数是(x-2)4中的x的系数乘以(x+1)4的常数项加上(x-2)4中的常数项乘以(x+1)4中的x的系数
∵(x-2)4展开式的通项为Tr+1=(-2)rC4rx4-r
令4-r=0得r=4,其常数项为16;令4-r=1得r=3所以其展开式含x的系数为-32
∵(x+1)4展开式的通项为Tk+1=C4kxk
∴展开式的常数项为1;含x的系数为4
∴展开的多项式中,x项的系数是16×4-32=32
故答案为32
点评:本题考查等价转化的思想方法、考查利用二项展开式的通项公式解决二项展开式的特定项问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
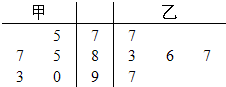 (2012•江门一模)甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示.
(2012•江门一模)甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示.