Question

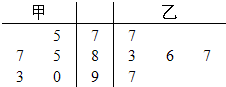（2012•江门一模）甲、乙两名同学在5次英语口语测试中的成绩统计如图的茎叶图所示．
（1）现要从中选派一人参加英语口语竞赛，从两同学的平均成绩和方差分析，派谁参加更合适；
（2）若将频率视为概率，对学生甲在今后的三次英语口语竞赛成绩进行预测，记这三次成绩中高于80分的次数为ξ，求ξ的分布列及数学期望Eξ．
（注：样本数据x₁，x₂，…，x_n的方差s²=

1

n

[(x1-

.

x

)2+(x2-

.

x

)2+…+(xn-

.

x

)2]，其中

.

x

表示样本均值）

Answer 1

分析：（1）根据茎叶图的数据，利用平均数及方差公式，即可求得结论；
（2）求得ξ取值及ξ～（3，

4

5

），求出相应概率，可得ξ的分布列，从而可求数学期望Eξ．

解答：解：（1）

.

x甲

=

75+85+87+90+93

5

=86…（1分），

.

x乙

=

77+83+86+87+97

5

=86…（2分），
s甲2=

1

5

[(75-86)2+(85-86)2+(87-86)2+(90-86)2+(93-86)2]=37.6…（3分），
s乙2=

1

5

[(77-86)2+(83-86)2+(86-86)2+(87-86)2+(97-86)2]=42.4…（4分），
因为

.

x甲

=

.

x乙

，s甲2＜s乙2，所以派甲去更合适…（5分）．
（2）甲高于80分的频率为

4

5

，从而每次成绩高于80分的概率P=

4

5

…（6分），
ξ取值为0，1，2，3，ξ～（3，

4

5

）…（7分），
直接计算得P（ξ=0）=

C

0 3

×(

4

5

)0×(

1

5

)3=

1

125

；P（ξ=1）=

C

1 3

×(

4

5

)1×(

1

5

)2=

12

125

；
P（ξ=2）=

C

2 3

×(

4

5

)2×(

1

5

)1=

48

125

；P（ξ=3）=

C

3 3

×(

4

5

)3×(

1

5

)0=

64

125

，…（11分），
ξ的分布列为

ξ	0	1	2	3
P	1 125	12 125	48 125	64 125

所以，Eξ=0×

1

125

+1×

12

125

+2×

48

125

+3×

64

125

=

12

5

，…（14分）

点评：本题考查概率与统计，考查茎叶图的运用，考查随机变量的分布列与期望，确定变量的取值，求出概率是关键．