题目内容
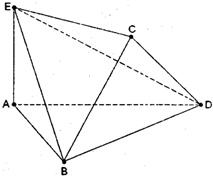
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=
.
(Ⅰ)求证:DE⊥AC;
(Ⅱ)求DE与平面BEC所成角的正弦值;
(Ⅲ)直线BE上是否存在一点M,使得CM∥平面ADE,若存在,求点M的位置,不存在请说明理由.
分析:(Ⅰ)借助空间向量来证 DE⊥AC,只需在空间直角坐标系下,证明
•=0 即可.以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系,再写出定点E,A,B,D的坐标,求出C点坐标,向量
,
坐标,再计算(Ⅱ)
•,看是否为0.
(Ⅱ)DE与平面BEC所成角,也即DE与平面BCE的法向量所成角的余角,设平面BCE的法向量为
=(x,y,z) 则
根据法向量与平面内任意向量垂直,即可求出平面BCE的法向量坐标,再求平面BCE的法向量与DE所成角,最后求出该角的余角即可.
(III)先假设直线BE上存在一点M,使得CM∥平面ADE,向量
垂直于平面ADE的法向量,再利用垂直时数量积为0来计算.如能计算出参数λ的值,则存在,否则,不存在.
解答: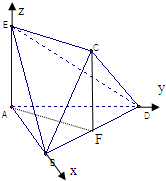
解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系
则E(0,0,
),B(2,0,0)D(0,2,0),
做BD的中点F并连接CF,AF;由题意可得CF⊥BD且AF=CF=
又∵平面BDA⊥平面BDC,∴CF⊥平面BDA,
所以C的坐标为C(1,1,
)
∴
=(0,-2,
),
=(1,1,
)
∴
•=(0,-2,
)•(1,1,
)=0
故DE⊥AC
(Ⅱ)设平面BCE的法向量为
=(x,y,z) 则
,即
∴
令x=1得
=(1,-1,
) 又
=(0,-2,
)
设平面DE与平面BCE所成角为θ,则
sinθ=|cos<
,
>|=
=
(III)假设存在点M使得CM∥面ADE,则
=
λ=(2,0,-
),∴
=(2λ,0,-
λ) 得M(2λ,0,
-λ)
又因为AE⊥平面ABD,AB⊥AD 所以AB⊥平面ADE
因为CM∥面ADE,则
⊥ 即
•=0得2λ-1=0∴λ=
故点M为BE的中点时CM∥面ADE.
点评:夲题考查了用空间向量求证线线垂直,线面平行,以及线面角,属于常规题,需掌握.
 涓€棰樹竴棰樻壘绛旀瑙f瀽澶參浜�
涓€棰樹竴棰樻壘绛旀瑙f瀽澶參浜�
涓嬭浇浣滀笟绮剧伒鐩存帴鏌ョ湅鏁翠功绛旀瑙f瀽绔嬪嵆涓嬭浇
练习册系列答案
相关题目
 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE= 解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系
解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系 解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系
解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
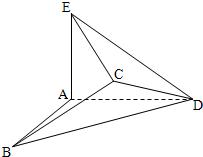 若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).
若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).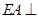 平面ABD,AE=a。
平面ABD,AE=a。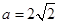 ,求证:AB//平面CDE;
,求证:AB//平面CDE;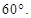
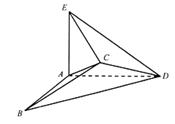
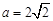 ,求证:AB//平面CDE;
,求证:AB//平面CDE;