题目内容
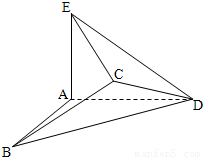
若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).
(Ⅰ)若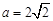 ,求证:AB//平面CDE;
,求证:AB//平面CDE;
(Ⅱ)求实数a的值,使得二面角A-EC-D的大小为60°.

【答案】
解:(1)如图建立空间指教坐标系,则
A(0,0,0),B(2,0,0),C(1,1,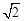 ),D(0,2,0),E(0,0,
),D(0,2,0),E(0,0,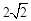 ),
),
 2分
2分
设平面 的一个法向量为
的一个法向量为 ,则有
,则有 ,
,
取 时,
时,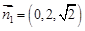 4分
4分
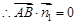 ,又
,又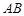 不在平面
不在平面 内,所以
内,所以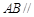 平面
平面 ; 7分
; 7分
(2)如图建立空间直角坐标系,则
A(0,0,0),B(2,0,0),C(1,1,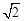 ),D(0,2,0),E(0,0,
),D(0,2,0),E(0,0,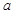 ),
),
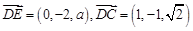 ,
,
设平面 的一个法向量为
的一个法向量为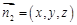 ,则有
,则有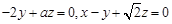 ,
,
取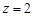 时,
时,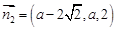 9分
9分
又平面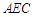 的一个法向量为
的一个法向量为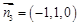 , 10分
, 10分
因为二面角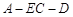 的大小为
的大小为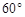 ,
,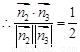 ,
,
即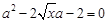 ,解得
,解得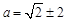 14分
14分
又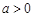 ,所以
,所以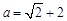 . 15分
. 15分
注:几何解法相应给分.
【解析】略

练习册系列答案
相关题目
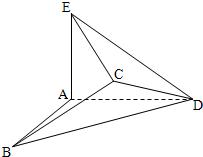 若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).
若将边长为2的正方形ABCD沿对角线BD折成一个直二面角,且EA⊥平面ABD,AE=a(如图).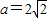 ,求证:AB∥平面CDE;
,求证:AB∥平面CDE;
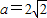 ,求证:AB∥平面CDE;
,求证:AB∥平面CDE;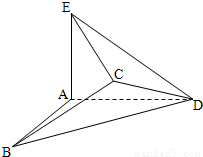
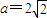 ,求证:AB∥平面CDE;
,求证:AB∥平面CDE;