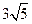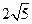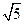题目内容
(14分)已知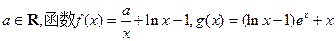 (其中e为自然对数的底数)。
(其中e为自然对数的底数)。
(1)求函数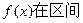
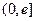 上的最小值;
上的最小值;
(2)是否存在实数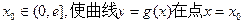 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出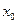 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
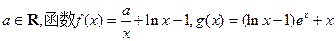 (其中e为自然对数的底数)。
(其中e为自然对数的底数)。(1)求函数
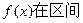
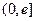 上的最小值;
上的最小值;(2)是否存在实数
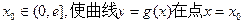 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出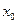 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。(1)当
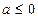 时,函数
时,函数 在区间
在区间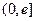 上无最小值;当
上无最小值;当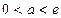 时,函数
时,函数 在区间
在区间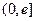 上的最小值为
上的最小值为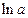
(2)故不存在
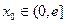 ,使曲线
,使曲线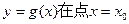 处的切线与
处的切线与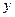 轴垂直
轴垂直解:(1)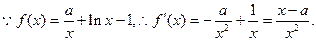
令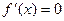 ,得
,得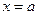 …………1分
…………1分
①若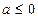 ,则
,则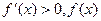 在区间
在区间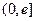 上单调递增,此时函数
上单调递增,此时函数 无最小值
无最小值
……2分
②若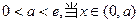 时,
时,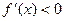 ,函数
,函数 在区间
在区间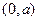 上单调递减
上单调递减
当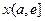 时,
时,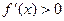 ,函数
,函数 在区间
在区间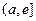 上单调递增
上单调递增
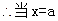 时,函数
时,函数 取得最小值
取得最小值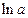 …………4分
…………4分
③若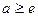 ,则
,则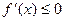 ,函数
,函数 在区间
在区间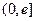 上单调递减
上单调递减
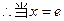 时,函数
时,函数 取得最小值
取得最小值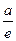 …………5分
…………5分
综上可知,当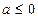 时,函数
时,函数 在区间
在区间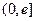 上无最小值;当
上无最小值;当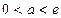 时,函数
时,函数 在区间
在区间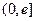 上的最小值为
上的最小值为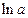 ;
;
当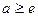 时,函数
时,函数 在区间
在区间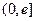 上的最小值为
上的最小值为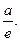 …………6分
…………6分
(2)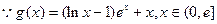
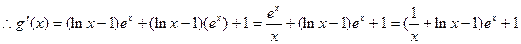
……7分
由(1)可知,当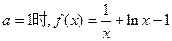
此时 在区间
在区间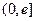 上的最小值为
上的最小值为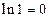
即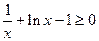 …………9分
…………9分
当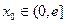 ,
,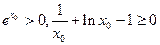
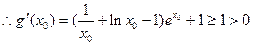 …………12分
…………12分
曲线y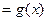 在点
在点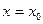 处的切线与
处的切线与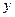 轴垂直等价于方程
轴垂直等价于方程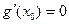 有实数解
有实数解
而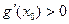 ,即方程
,即方程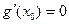 无实数解
无实数解
故不存在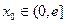 ,使曲线
,使曲线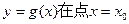 处的切线与
处的切线与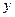 轴垂直…………
轴垂直…………
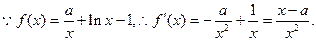
令
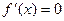 ,得
,得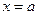 …………1分
…………1分①若
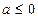 ,则
,则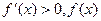 在区间
在区间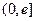 上单调递增,此时函数
上单调递增,此时函数 无最小值
无最小值……2分
②若
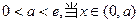 时,
时,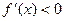 ,函数
,函数 在区间
在区间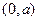 上单调递减
上单调递减当
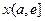 时,
时,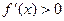 ,函数
,函数 在区间
在区间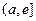 上单调递增
上单调递增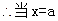 时,函数
时,函数 取得最小值
取得最小值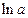 …………4分
…………4分③若
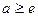 ,则
,则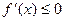 ,函数
,函数 在区间
在区间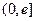 上单调递减
上单调递减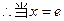 时,函数
时,函数 取得最小值
取得最小值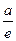 …………5分
…………5分综上可知,当
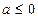 时,函数
时,函数 在区间
在区间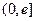 上无最小值;当
上无最小值;当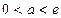 时,函数
时,函数 在区间
在区间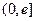 上的最小值为
上的最小值为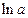 ;
;当
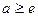 时,函数
时,函数 在区间
在区间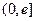 上的最小值为
上的最小值为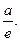 …………6分
…………6分(2)
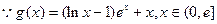
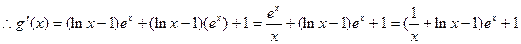
……7分
由(1)可知,当
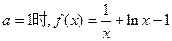
此时
 在区间
在区间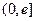 上的最小值为
上的最小值为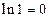
即
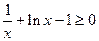 …………9分
…………9分当
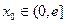 ,
,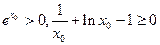
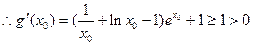 …………12分
…………12分曲线y
 在点
在点 处的切线与
处的切线与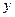 轴垂直等价于方程
轴垂直等价于方程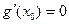 有实数解
有实数解而
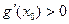 ,即方程
,即方程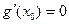 无实数解
无实数解故不存在
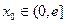 ,使曲线
,使曲线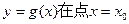 处的切线与
处的切线与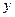 轴垂直…………
轴垂直…………
练习册系列答案
相关题目

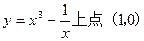 处的切线方程
处的切线方程 是____________
是____________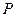 在曲线
在曲线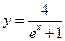 上,
上,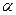 为曲线在点
为曲线在点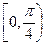
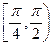
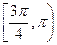
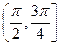
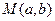 是曲线
是曲线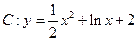 上的任意一点,直线
上的任意一点,直线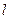 是曲线
是曲线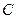 在点
在点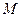 处的切线,那么直线
处的切线,那么直线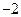
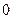
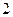
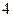
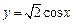 在
在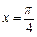 处的切线方程是
处的切线方程是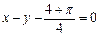
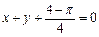
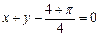
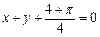
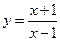 在点
在点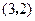 处的切线与直线
处的切线与直线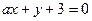 垂直,则
垂直,则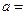 ( )
( )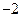
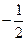
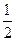
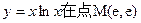 处切线在
处切线在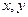 轴上的截距分别为
轴上的截距分别为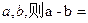 ( )
( )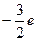
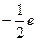
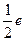

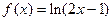 上的点到直线
上的点到直线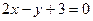 的最短距离是 ( )
的最短距离是 ( )