Question

正方形ABCD的边长是2，E、F分别是AB和CD的中点，将正方形沿EF折成直二面角（如图所示）.M为矩形AEFD内一点，如果∠MBE=∠MBC，MB和平面BCF所成角的正切值为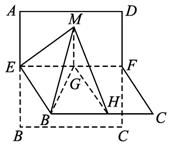，那么点M到直线EF的距离为（    ）

A.                 B.1                C.                D.

Answer 1

解析:作MG⊥EF,

∵平面AEF⊥平面EBCF,∴MG⊥平面EBCF.∴∠MBG是MB和平面BCF所成的角.

    作GH⊥BC，则MH⊥BH.

∵∠MBH=∠MBE，

∴Rt△MEB≌Rt△MHB.

∴ME=MC.∴EG=GH,

    即G为EF的中点.

    又=，

∴MG=BG==.

答案:A