题目内容
正方形ABCD的边长为4,中心为M,球O与正方形ABCD所在的平面相切于M点,过点M的球的直径另一端点为N,线段NA与球O的球面的交点为E,且E恰为线段NA的中点,则球O的体积为( )
分析:由题意判断直角三角形为等腰直角三角形,求出球的直径,然后求出半径,即可求解球的体积.
解答: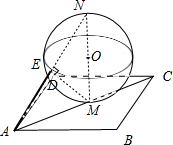 解:因为正方形ABCD的边长为4,中心为M,球O与正方形ABCD所在的平面相切于M点,
解:因为正方形ABCD的边长为4,中心为M,球O与正方形ABCD所在的平面相切于M点,
过点M的球的直径另一端点为N,所以MN⊥平面ABCD,且O∈MN,线段NA与球O的球面的交点为E,且E恰为线段NA的中点,
所以∠MEN=90°.并且EN=EM,
所以AM=MN,因为正方形ABCD的边长为4,
所以AM=MN=2
,所以球的直径为2
,球的半径为:
.
球的体积为:
×(
)3=
π.
故选B.
 解:因为正方形ABCD的边长为4,中心为M,球O与正方形ABCD所在的平面相切于M点,
解:因为正方形ABCD的边长为4,中心为M,球O与正方形ABCD所在的平面相切于M点,过点M的球的直径另一端点为N,所以MN⊥平面ABCD,且O∈MN,线段NA与球O的球面的交点为E,且E恰为线段NA的中点,
所以∠MEN=90°.并且EN=EM,
所以AM=MN,因为正方形ABCD的边长为4,
所以AM=MN=2
| 2 |
| 2 |
| 2 |
球的体积为:
| 4π |
| 3 |
| 2 |
8
| ||
| 3 |
故选B.
点评:本题考查球的体积的求法,空间想象能力,计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.
如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.