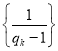题目内容
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的斜率为3,求实数
处的切线的斜率为3,求实数![]() 的值;
的值;
(2)若函数在区间![]() 上存在极小值,求实数
上存在极小值,求实数![]() 的取值范围;
的取值范围;
(3)如果![]() 的解集中只有一个整数,求实数
的解集中只有一个整数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)先求出![]() ,利用
,利用![]() 可求
可求![]() .
.
(2)因函数在区间![]() 上存在极小值,故
上存在极小值,故![]() 在
在![]() 上有解,利用求根公式求出
上有解,利用求根公式求出![]() 的较大的根,它在区间
的较大的根,它在区间![]() 中,从而得到
中,从而得到![]() 的取值范围,
的取值范围,
(3)利用导数可得当![]() 时,
时,![]() 为
为![]() 上的增函数,而
上的增函数,而![]() ,故
,故![]() 无整数解;当
无整数解;当![]() 时,因
时,因![]() 在
在![]() 上有两个不同的解
上有两个不同的解![]() 且
且![]() ,所以
,所以![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,结合
上为增函数,结合![]() 可以得到
可以得到![]() ,从而得到
,从而得到![]() 的取值范围.
的取值范围.
(1)由题意,![]() ,
,
由题意知,![]() ,所以
,所以![]() ,解得
,解得![]() .
.
(2)令![]() ,所以
,所以![]() ,所以
,所以![]() (舍负),
(舍负),
因为函数在![]() 上存在极小值,所以
上存在极小值,所以![]() ,
,
解之得![]() ,
,
经检验,当![]() 时,符合题意,
时,符合题意,
所以![]() .
.
(3)①当![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,
![]() 在
在![]() 上为增函数,
上为增函数,![]() .
.
所以当![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() ,所以
,所以![]() 无整数解;
无整数解;
②当![]() ,即
,即![]() 或
或![]() 时,
时,
若![]() ,则
,则![]() ,同①可得
,同①可得![]() 无整数解;
无整数解;
若![]() ,
,![]() 即
即![]() 在
在![]() 上有两个不同的解
上有两个不同的解![]() 且
且![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数;
上为减函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,
而![]() ,所以
,所以![]() 在
在![]() 上无解,故
上无解,故![]() 在
在![]() 上只有一个整数解,
上只有一个整数解,
故![]() ,即
,即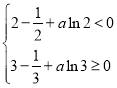 ,
,
解得![]() ,
,
综上,![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()