题目内容
E、F分别是正方形ABCD的边AB和CD的中点,EF交BD于O,以EF为棱将正方形折成直二面角,则∠BOD=
120°
120°
.分析:连接ED、BD并设翻折前正方形ABCD的边长为2,可得BO=DO=
,Rt△DEF中算出ED=
.根据面面平行的性质得到BE⊥平面AEFD,从而得到BE⊥ED.Rt△BED中,利用勾股定理算出BD=
,最后在△BOD中,由余弦定理得cos∠BOD即可
| 2 |
| 5 |
| 6 |
解答: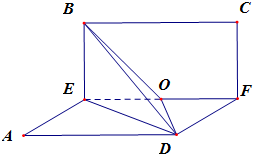 解:设翻折前正方形ABCD的边长为2,
解:设翻折前正方形ABCD的边长为2,
连接ED、BD,则
∵平面AEFD⊥平面BCFE,平面AEFD∩平面BCFE=EF,BE⊥EF
∴BE⊥平面AEFD,结合DE?平面AEFD可得BE⊥ED
∵Rt△DEF中,EF=BC=2,DF=1
∴ED=
=
由此可得Rt△BED中,BD=
=
∵△BOD中,BO=DO=
,
∴由余弦定理,得cos∠BOD=
=
=-
∵∠BOD是三角形内角,∴∠BOD=120°
故答案为:120°
 解:设翻折前正方形ABCD的边长为2,
解:设翻折前正方形ABCD的边长为2,连接ED、BD,则
∵平面AEFD⊥平面BCFE,平面AEFD∩平面BCFE=EF,BE⊥EF
∴BE⊥平面AEFD,结合DE?平面AEFD可得BE⊥ED
∵Rt△DEF中,EF=BC=2,DF=1
∴ED=
| EF2+DF2 |
| 5 |
由此可得Rt△BED中,BD=
| ED2+BE2 |
| 6 |
∵△BOD中,BO=DO=
| 2 |
∴由余弦定理,得cos∠BOD=
| BO2+DO2-BD2 |
| 2×BO×DO |
| 2+2-6 | ||||
2×
|
| 1 |
| 2 |
∵∠BOD是三角形内角,∴∠BOD=120°
故答案为:120°
点评:本题以正方形的翻折为例,求翻折后BO、DO所成角大小,着重考查了线面垂直、面面垂直的性质和余弦定理等知识点,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
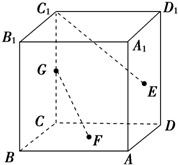 如右图所示,正方体ABCD-A1B1C1D1中,E、F分别是正方形ADD1A1和ABCD的中心,G是CC1的中点,设GF、C1E与AB所成的角分别为α、β,则α+β等于( )
如右图所示,正方体ABCD-A1B1C1D1中,E、F分别是正方形ADD1A1和ABCD的中心,G是CC1的中点,设GF、C1E与AB所成的角分别为α、β,则α+β等于( )| A、120° | B、60° | C、75° | D、90° |
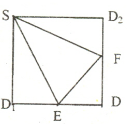 如图,E、F分别是正方形SD1DD2的边D1D、DD2的中点,沿SE、SF、EF将它折成一个几何体,使D1、D、D2重合,记作D,给出下列位置关系:①SD⊥面EFD; ②SE⊥面EFD;③DF⊥SE;④EF⊥面SED.其中成立的有( )
如图,E、F分别是正方形SD1DD2的边D1D、DD2的中点,沿SE、SF、EF将它折成一个几何体,使D1、D、D2重合,记作D,给出下列位置关系:①SD⊥面EFD; ②SE⊥面EFD;③DF⊥SE;④EF⊥面SED.其中成立的有( )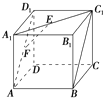 正方体ABCD-A1B1C1D1,E、F分别是正方形A1B1C1D1和ADD1A1的中心,则EF和CD所成的角是( )
正方体ABCD-A1B1C1D1,E、F分别是正方形A1B1C1D1和ADD1A1的中心,则EF和CD所成的角是( )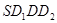 的边
的边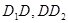 的中点,沿SE、SF、EF将它折成一个几何体,使
的中点,沿SE、SF、EF将它折成一个几何体,使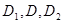 重合,记作D,给出下列位置关系:①SD
重合,记作D,给出下列位置关系:①SD 面EFD ; ②SE
面EFD ; ②SE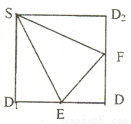
 、
、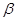 ,则
,则