题目内容
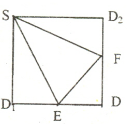如图，E、F分别是正方形SD1DD2的边D1D、DD2的中点，沿SE、SF、EF将它折成一个几何体，使D1、D、D2重合，记作D，给出下列位置关系：①SD⊥面EFD； ②SE⊥面EFD；③DF⊥SE；④EF⊥面SED．其中成立的有（ ）分析：画出图形，折叠前后，同一半平面的几何关系不变，利用三垂线定理判断选项即可．
解答：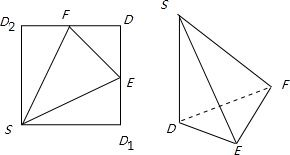
解：由题意，折叠前后，同一半平面的几何关系不变，
∵SD⊥DF，SD⊥DE，DE⊥DF，DE=DF
∴①SD⊥面EFD，即①正确；
②SE∩面EFD，但不垂直，即②错误；
③DF⊥平面SDE，故DF⊥SE，即③正确；
④EF∩面SED，但不垂直，即④错误．
故选B．
解：由题意，折叠前后，同一半平面的几何关系不变，∵SD⊥DF，SD⊥DE，DE⊥DF，DE=DF
∴①SD⊥面EFD，即①正确；
②SE∩面EFD，但不垂直，即②错误；
③DF⊥平面SDE，故DF⊥SE，即③正确；
④EF∩面SED，但不垂直，即④错误．
故选B．
点评：本题考查几何图形的折叠与展开，考查空间想象能力，逻辑思维能力，是基础题．
练习册系列答案
相关题目
如图，棱长为1的正四面体ABCD中，E、F分别是棱AD、CD的中点，O是点A在平面BCD内的射影．
如图正三棱锥S-ABC的侧棱与底面边长相等，如果E、F分别是SC、AB的中点，那么异面直线EF与SA所成的角为
相等的向量．
平行的向量．
相等的向量．