题目内容
2.已知等差数列{an}满足a2=2,a5=8(1)求数列{an}的通项公式;
(2)设各项均为正数的等比数列bn}的前n项和为Tn若b3=a3,T2=3,求Tn.
分析 (1)设等差数列列{an}的公差为d,运用等差数列的通项公式,解方程可得首项和公差,即可得到所求通项公式;
(2)设各项均为正数的等比数列{bn}的公比为q(q>0),运用等比数列的通项公式,解方程可得首项和公比,即可得到所求通项公式和求和公式.
解答 解:(1)设等差数列列{an}的公差为d,由a2=2,a5=8
可得a1+d=2,a1+4d=8,
解得a1=2,d=2,
∴数列{an}的通项公式an=a1+(n-1)d=2n-2;
(2)设各项均为正数的等比数列{bn}的公比为q(q>0),
由(1)知a3=4,
则b3=a3=4,T2=3,即q≠1,
即有b1q2=4,b1+b1q=3,解得b1=1,q=2或b1=9,q=-$\frac{2}{3}$(舍去),
则bn=b1qn-1=2n-1,Tn=$\frac{1-{2}^{n}}{1-2}$=2n-1.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,考查方程思想的运用,属于基础题.

练习册系列答案
相关题目
13.若等比数列前n项和为${S_n}={2^{n+1}}-c$,则c等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | 0 |
10.在数列{an}中,已知${a_{n+1}}={a_n}+\frac{n}{2}$,且a1=2,则a99的值为( )
| A. | 2477 | B. | 2427 | C. | 2427.5 | D. | 2477.5 |
7.若复数Z满足Z=i(1-i),求|Z|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
14.在平行四平行边形OABC中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}$=2$\overrightarrow{MA}$,N为BC的中点,则$\overrightarrow{MN}$=( )
| A. | $\frac{1}{2}$$\overrightarrow{c}$-$\frac{1}{6}$$\overrightarrow{a}$ | B. | $\overrightarrow{c}$-$\frac{1}{6}$$\overrightarrow{a}$ | C. | $\frac{3}{2}$$\overrightarrow{a}$-$\overrightarrow{c}$ | D. | $\overrightarrow{a}$+$\frac{1}{2}$$\stackrel{c}{→}$ |
11.函数$f(x)=\frac{1}{{\sqrt{1-{2^x}}}}$的定义域是( )
| A. | {x|x≥0} | B. | {x|x≤0} | C. | {x|x>0} | D. | {x|x<0} |
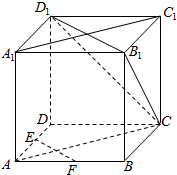 如图,在正方体ABCD-A1B1C1D1中,E,F分别为棱AD,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E,F分别为棱AD,AB的中点.