题目内容

12．函数f（x）=lg（1-x）+$\frac{1}{{\sqrt{x+2}}}$的定义域为（-2，1）．

分析 由分母中根式内部的代数式大于0，对数式的真数大于0联立不等式组得答案．

解答 解：由$\left\{\begin{array}{l}{1-x＞0}\\{x+2＞0}\end{array}\right.$，解得：-2＜x＜1．
∴函数f（x）=lg（1-x）+$\frac{1}{{\sqrt{x+2}}}$的定义域为（-2，1）．
故答案为：（-2，1）．

点评 本题考查函数的定义域及其求法，是基础的计算题．

练习册系列答案
相关题目
3．已知M（-2，1），N（2，3），则以MN为斜边的直角三角形的直角顶点P的轨迹方程是（　　）
A．x2+（y-2）2=5B．x2+（y-2）2=15
C．x2+（y-2）2=5（x≠2y-4）D．x2+（y-2）2=15（x≠2y-4）
3．若偶函数f（x）在（-∞，0]上单调递减，a=f（log23），b=f（log45），c=f（2${\;}^{\frac{3}{2}}$），则a，b，c满足（　　）
A．a＜b＜cB．b＜a＜cC．c＜a＜bD．c＜b＜a
20．已知tan2x-tanx-6=0，且x为第四象限角，试求：
（1）sinxcos（π-x）的值； 
（2）2cosx-sinx的值．
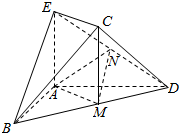7．如图，在几何体ABDCE中，AB=AD，AE⊥平面ABD，M为线段BD的中点，MC∥AE，AE=MC．
（1）求证：平面BCD⊥平面CDE；
（2）若N为线段DE的中点，求证：平面AMN∥平面BEC．
17．（Ⅰ）若x＞0，求f（x）=$\frac{12}{x}+3x$的最小值．
（Ⅱ）已知0＜x＜$\frac{1}{3}$，求f（x）=x（1-3x）的最大值．
4．（1）已知a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$=3，求下列各式的值．
①a+a-1；   
②a2+a-2．
（2）计算（2$\frac{7}{9}$）0+（0.1）-1+lg$\frac{1}{50}$-lg2+（$\frac{1}{7}$）-1+log75的值．
1．设函数f（x）=x2+ax+b，（a，b∈R）．
（Ⅰ）当b=$\frac{{a}^{2}}{4}$+1时，求函数f（x）在[-1，1]上的最小值g（a）的表达式；
（Ⅱ）若b=a+1且函数f（x）在[-1，1]上存在两个不同零点，试求实数a的取值范围．
（Ⅲ）若b=a+1且函数f（x）在[-1，1]上存在一个零点，试求实数a的取值范围．
2．已知等差数列{an}满足a2=2，a5=8
（1）求数列{an}的通项公式；
（2）设各项均为正数的等比数列bn}的前n项和为Tn若b3=a3，T2=3，求Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网