题目内容
已知椭圆C1: +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,直线l:x-y+
,直线l:x-y+ =0与椭圆C1相切.
=0与椭圆C1相切.(1)求椭圆C1的方程;
(2)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直与椭圆的长轴,动直线l2垂直于直线l1于点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;
(3)若A(x1,2),B(x2,y2),C(x,y)是C2上不同的点,且AB⊥BC,求实数y的取值范围.
【答案】分析:(1)因为e= ,椭圆 C1的方程可设为
,椭圆 C1的方程可设为 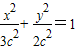 ,与直线方程 x-y+
,与直线方程 x-y+ =0 联立,由判别式等于0解出c值,即得椭圆 C1的方程.
=0 联立,由判别式等于0解出c值,即得椭圆 C1的方程.
(2)由题意可知,点M的轨迹C2 是以直线 l1 为准线,点F2为焦点的抛物线,由直线l1的方程为X=-1,点P的坐标为(1,0),可得点M的轨迹C2 的方程为 y2=4x.
(3)由题意可知A点坐标为(1,2),由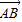 •
•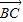 =0,可得(x2-1,y2-1)•(x-x2,y-y2 )=0,方程 y22+(2+y )y2+(2y+16)=0 有不为2的解,故 y2-4y-60≥0,且y≠-6,从而解得 y 的取值范围.
=0,可得(x2-1,y2-1)•(x-x2,y-y2 )=0,方程 y22+(2+y )y2+(2y+16)=0 有不为2的解,故 y2-4y-60≥0,且y≠-6,从而解得 y 的取值范围.
解答:解:(1)因为e=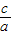 =
=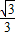 ,所以,a=
,所以,a= c,b=
c,b= c,椭圆 C1的方程可设为
c,椭圆 C1的方程可设为 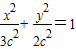 ,
,
与直线方程 x-y+ =0 联立,消去y,可得 5x2+6
=0 联立,消去y,可得 5x2+6 x+15-6c2=0,
x+15-6c2=0,
因为直线与椭圆相切,所以,△=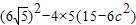 =0,
=0,
又因为c>0,所以 c=1,所以,椭圆 C1的方程为 .
.
(2)由题意可知,PM=MF2,又PM为点M到直线l1 的距离,
所以,点M到直线l1的距离与到点 F2的距离相等,
即点M的轨迹C2 是以直线 l1 为准线,点F2为焦点的抛物线,
因为直线l1的方程为X=-1,点P的坐标为(1,0),所以,点M的轨迹C2 的方程为 y2=4x.
(3)由题意可知A点坐标为(1,2). 因为AB⊥BC,所以, •
• =0,
=0,
即 (x2-1,y2-1)•(x-x2,y-y2 )=0,又因为 ,
,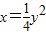 ,
,
所以,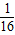 (y22-4 )(y2-y22 )+(y2-2 )(y-y2 )=0,
(y22-4 )(y2-y22 )+(y2-2 )(y-y2 )=0,
因为 y2≠2,y2≠y,所以,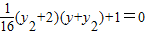 ,
,
整理可得:y22+(2+y )y2+(2y+16)=0,关于 y2 的方程有不为2的解,所以
△=(2+y)2-4(2y+16)≥0,且 y≠-6,
所以,y2-4y-60≥0,且y≠-6,解得 y 的取值范围为 y<-6,或 y≥10.
点评:本题考查求椭圆的标准方程,直线和椭圆的位置关系的应用,式子的化简变形是解题的易错点.
 ,椭圆 C1的方程可设为
,椭圆 C1的方程可设为 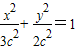 ,与直线方程 x-y+
,与直线方程 x-y+ =0 联立,由判别式等于0解出c值,即得椭圆 C1的方程.
=0 联立,由判别式等于0解出c值,即得椭圆 C1的方程.(2)由题意可知,点M的轨迹C2 是以直线 l1 为准线,点F2为焦点的抛物线,由直线l1的方程为X=-1,点P的坐标为(1,0),可得点M的轨迹C2 的方程为 y2=4x.
(3)由题意可知A点坐标为(1,2),由
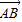 •
•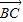 =0,可得(x2-1,y2-1)•(x-x2,y-y2 )=0,方程 y22+(2+y )y2+(2y+16)=0 有不为2的解,故 y2-4y-60≥0,且y≠-6,从而解得 y 的取值范围.
=0,可得(x2-1,y2-1)•(x-x2,y-y2 )=0,方程 y22+(2+y )y2+(2y+16)=0 有不为2的解,故 y2-4y-60≥0,且y≠-6,从而解得 y 的取值范围.解答:解:(1)因为e=
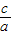 =
=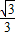 ,所以,a=
,所以,a= c,b=
c,b= c,椭圆 C1的方程可设为
c,椭圆 C1的方程可设为 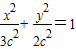 ,
,与直线方程 x-y+
 =0 联立,消去y,可得 5x2+6
=0 联立,消去y,可得 5x2+6 x+15-6c2=0,
x+15-6c2=0,因为直线与椭圆相切,所以,△=
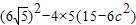 =0,
=0,又因为c>0,所以 c=1,所以,椭圆 C1的方程为
 .
.(2)由题意可知,PM=MF2,又PM为点M到直线l1 的距离,
所以,点M到直线l1的距离与到点 F2的距离相等,
即点M的轨迹C2 是以直线 l1 为准线,点F2为焦点的抛物线,
因为直线l1的方程为X=-1,点P的坐标为(1,0),所以,点M的轨迹C2 的方程为 y2=4x.
(3)由题意可知A点坐标为(1,2). 因为AB⊥BC,所以,
 •
• =0,
=0,即 (x2-1,y2-1)•(x-x2,y-y2 )=0,又因为
 ,
,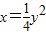 ,
,所以,
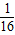 (y22-4 )(y2-y22 )+(y2-2 )(y-y2 )=0,
(y22-4 )(y2-y22 )+(y2-2 )(y-y2 )=0,因为 y2≠2,y2≠y,所以,
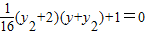 ,
,整理可得:y22+(2+y )y2+(2y+16)=0,关于 y2 的方程有不为2的解,所以
△=(2+y)2-4(2y+16)≥0,且 y≠-6,
所以,y2-4y-60≥0,且y≠-6,解得 y 的取值范围为 y<-6,或 y≥10.
点评:本题考查求椭圆的标准方程,直线和椭圆的位置关系的应用,式子的化简变形是解题的易错点.

练习册系列答案
相关题目
 =1 (a>b>0)与双曲线C2:x2-
=1 (a>b>0)与双曲线C2:x2-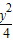 =1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )

 +
+ =1(a>b>0)的长轴长为4,离心率为
=1(a>b>0)的长轴长为4,离心率为 ,F1、F2分别为其左右焦点.一动圆过点F2,且与直线x=-1相切.
,F1、F2分别为其左右焦点.一动圆过点F2,且与直线x=-1相切. 共线,
共线, 与
与 共线,且
共线,且 •
• =0,求四边形PMQN面积的最小值.
=0,求四边形PMQN面积的最小值. =1(a>b>0)的左、右焦点分别为F1、F2,其中F2也是抛物线C2:y2=4x的焦点,M是C1与C2在第一象限的交点,且
=1(a>b>0)的左、右焦点分别为F1、F2,其中F2也是抛物线C2:y2=4x的焦点,M是C1与C2在第一象限的交点,且